[福建]2012届福建省永春县九年级上学期期末数学试卷
如图,在△ABC中,∠C=90o,AC=3,BC=4,则sinB的值是( )
A. ; ; |
B. ; ; |
C. ; ; |
D.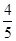 . . |

一个袋子中装有4只白球和3只红球,这些球除颜色外其余均相同,搅匀后,从袋子中随机摸出一个球是红球的概率是 ( )
A. ; ; |
B. ; ; |
C. ; ; |
D. |
若两个相似三角形的相似比为1:4,则它们的面积之比为 ( )
| A.1:2 ; | B. 1:4 ; | C.1:5 ; | D.1:16. |
二次函数 的图象如图所示.当
的图象如图所示.当 <0时,自变量
<0时,自变量 的取值范围是( ).
的取值范围是( ).
A.-1< <3; <3; |
B. <-1; <-1; |
C. >3; >3; |
D. <-1或 <-1或 >3. >3. |
如下图是某种计算程序示意图,初始端输入 后经式子
后经式子 处理后得到一个结果.若这个结果大于0,则输出此结果;否则就将第一次得到的结果作为输入的
处理后得到一个结果.若这个结果大于0,则输出此结果;否则就将第一次得到的结果作为输入的 再次运行程序…直到输出结果为止.
再次运行程序…直到输出结果为止.
(1)当初始端输入 =-1时,输出的结果是 ;
=-1时,输出的结果是 ;
(2)若该程序满足条件:存在实数 ,当初始端输入
,当初始端输入 =
= 时,该程序的运算无法停止(即会一直循环运行)”,请写出一个符合条件的
时,该程序的运算无法停止(即会一直循环运行)”,请写出一个符合条件的 的值 .
的值 .
为了测量树的高度HD,在离树20米的C处,用高1.20米的测角仪AC测得树顶端H的仰角为35°,求树HD的高.(精确到0.1米)
在一个箱子中放有三张完全相同的卡片,卡片上分别标有数字1,2,3.从箱子中任意取出一张卡片,用卡片上的数字作为十位数字,放回后搅匀,再取出一张卡片,用卡片上的数字作为个位数字,这样组成一个两位数.
(1)请你用画树状图或列表的方法表示所有等可能的结果;
(2)组成的两位数是偶数的概率是多少?
在△ABC中,∠C=90°
(1)如图1,P是AC上的点,过点P作直线截△ABC,使截得的三角形与△ABC相似.
例如:过点P作PD∥BC交AB于D,则截得的△ADP与△ABC相似.请你在图中画出所有满足条件的直线.
(2)如图2,Q是BC上异于点B,C的动点,过点Q作直线截△ABC,使截得的三角形与△ABC相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)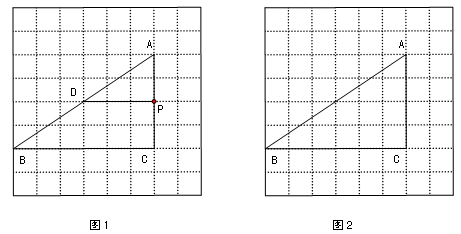
已知二次函数 的图象经过A(2,0)、B(0,-6)两点.
的图象经过A(2,0)、B(0,-6)两点.
(1)求这个二次函数的解析式;
(2)求该二次函数图象与 轴的另一个交点.
轴的另一个交点.
某商店经销一种成本为每千克40元的产品,若按每千克50元销售,一个月能售出500千克.销售单价每涨1元,月销售量就减少10千克,针对这种产品,请解答以下问题:
(1)当销售单价定为每千克55元时,计算销售量与月销售利润;
(2)商店想在销售额不超过20000元的情况下,使得月销售利润达到8000元,则销售单价应为多少?
已知抛物线 过点(8,0),
过点(8,0),

(1)求 的值;
的值;
(2)如图 ,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在
,在抛物线内作矩形ABCD,使点C、D落在抛物线上,点A、B落在 轴上,设矩形ABCD的周长为L,求L的最大值;
轴上,设矩形ABCD的周长为L,求L的最大值;
(3)如图 ,抛物线的顶点为E,对称轴与直线
,抛物线的顶点为E,对称轴与直线 交于点F.将直线EF向右平移
交于点F.将直线EF向右平移 个单位后(
个单位后( >0),交直线
>0),交直线 于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求
于点M,交抛物线于点N,若以E、F、M、N为顶点的四边形是平行四边形,求 的值.
的值.
如图1, 矩形铁片ABCD中,AD="8," AB="4;" 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
(1)直接写出矩形铁片ABCD的面积 ;
(2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
①证明四边形MNPQ是菱形;
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.
 ;
;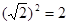 ;
;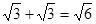 ;
; .
. 的解是( )
的解是( )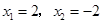 ;
;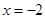 ;
;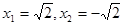 ;
;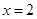 .
.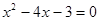 ,下列配方结果正确的是( )
,下列配方结果正确的是( )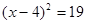 ;
;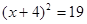 ;
; ;
;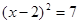 .
. 时,二次根式
时,二次根式 有意义.
有意义. .
. ,那么
,那么 .
.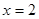 是方程
是方程 的根,则
的根,则 __________
__________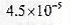 _.
_.
 ,3
,3
 ,可列方程为 .
,可列方程为 .



 粤公网安备 44130202000953号
粤公网安备 44130202000953号