[浙江]2011-2012学年浙江省杭州市坎山镇中下期期中考试七年级数学试卷
下列事件中,必然事件是( )
| A.任意掷一枚均匀的硬币,正面朝下 |
| B.上学的路上一定能遇到同班同学 |
| C.黑暗中任意从一串不同的钥匙中随意摸出一把,用它打开了门 |
| D.通常情况下,水往低入流 |
如图,从图甲到图乙的变换是( )
| A.轴对称变换 | B.平移变换 | C.旋转变换 | D.相似变换 |
 |
甲  乙
乙
若关于 的二元一次方程组
的二元一次方程组 的解也是二元一次方程
的解也是二元一次方程 的解,则
的解,则 的值为( )
的值为( )
A. |
B. |
C. |
D. |
如图,在ΔABC中,AD是ΔABC的高,AE是ΔABC的角平分线,已知∠BAC=82°,∠C=40°,则∠DAE的度数是( ) 
A. |
B. |
C. |
D. |
小明打算暑假里到上海世博会一日游,上午可以先从台湾馆、香港馆、韩国馆中随机抽一个馆,下午再从加拿大馆、法国馆、俄罗斯馆中随机抽一个馆游玩.则小明恰好上午选中台湾馆,下午选中法国馆这两个场馆的概率是( )
A. |
B. |
C. |
D. |
测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是( )
| A.边角边 | B.角边角 | C.边边角 | D.角角边 |
在△ABC中,∠C= 。两条角平分线AD,BE所在直线所成的角的度数是
。两条角平分线AD,BE所在直线所成的角的度数是
A. |
B. |
C. |
D. 或 或 |
把一根长为70cm的铁丝正好折成一个长方形,且长是宽的2倍,若设长为 cm,宽为
cm,宽为 cm,则由题意可列方程组是 。
cm,则由题意可列方程组是 。
如图,△ABC中,DE是AC的中垂线,AE=5cm,△ABC的周长为30cm,则△ABD的周长是 ;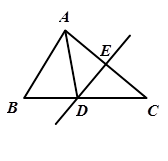
如图所示,已知∠B =∠D=90°,∠C=∠E, AB=AD。有下列结论:①BM= DN;②EM=CF;③∠BAM ="∠DA" N;④△ACM≌△AEN。其中正确的有 (填序号)
观察表中三角形个数的变化规律:
| 图形 |
 |
 |
 |
|
 |
| 横截线 条 数 |
0 |
1 |
2 |
… |
n |
| 三角形 个 数 |
6 |
? |
? |
… |
? |
若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有 条,
条,
则三角形的个数是______________(用含 的代数式表示)。
的代数式表示)。
如图,已知△ABC.只用直尺(没有刻度的尺)和圆规,求作一个△DEF,使得△DEF∽△ABC,且EF= BC.(要求保留作图痕迹,不必写出作法)
BC.(要求保留作图痕迹,不必写出作法)
如图,在△ABC和△DEF中,∠A=∠D,AC=DF,AE=BD,请说明∠C=∠F的理由。
在所给的网格图(每小格边长均为1的正方形)中,完成下列各题:
(1)将△ABC向右平移4个单位得到△A1B1C1;
(2)以直线 为对称轴作△ABC的轴对称图形△
为对称轴作△ABC的轴对称图形△ ;
;
(3)△ 可以看作是由△A1B1C1先向左平移4个单位,再以直线
可以看作是由△A1B1C1先向左平移4个单位,再以直线 为对称轴作轴对
为对称轴作轴对
称变换得到的。除此以外,△ 还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。
还可以看作是由△A1B1C1经怎样变换得到的?请选择一种方法,写出图形变换的步骤。

一个不透明的口袋里装有红、白、黄三种颜色的乒乓球(除颜色外其余都相同),其中有白球2个,黄球1个.
(1)若口袋中有3个红球,求从任意摸出一个球是白球的概率,并用列表或画树状图的方法说明;
(2)若从袋中任意摸出一球,摸到白球的概率为 ,求口袋中红球的个数.
,求口袋中红球的个数.
某公园门票是每人15元,若超过10人,可购买团体票,票价如下:
| 购买人数(人) |
10-50 |
51-100 |
100以上 |
| 每人门票价(元) |
13 |
11 |
9 |
有甲、乙两个旅游团,若分别购买门票,两团总计应付1314元;若合在一起购买门票,总计应付1008元,问这两个旅游团各有多少人?
 ,∠B=
,∠B=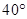 ,则∠C等于( )
,则∠C等于( )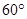






 ,若变形为用y表示的代数式表示x,则x= .
,若变形为用y表示的代数式表示x,则x= . ,则
,则







 粤公网安备 44130202000953号
粤公网安备 44130202000953号