[湖北]2012届初中毕业生学业考试(湖北黄石卷)数学
已知反比例函数 (
( 为常数),当
为常数),当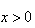 时,
时,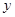 随
随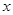 的增大而增大,则一次函数
的增大而增大,则一次函数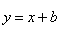 的图像不经过第几象限( )
的图像不经过第几象限( )
| A.一 | B.二 | C.三 | D.四 |
2012年5月某日我国部分城市的最高气温统计如下表所示:
| 城 市 |
武汉 |
成都 |
北京 |
上海 |
海南 |
南京 |
拉萨 |
深圳 |
| 气温(℃) |
27 |
27 |
24 |
25 |
28 |
28 |
23 |
26 |
请问这组数据的平均数是( )
A.24 B.25 C.26 D.27
如图(4)所示,直线 与线段
与线段 为直径的圆相切于点
为直径的圆相切于点 ,并交
,并交 的延长线于点
的延长线于点 ,且
,且 ,
, 点在切线
点在切线 上移动.当
上移动.当 的度数最大时,则
的度数最大时,则 的度数为( )
的度数为( )
A. ° ° |
B. ° ° |
C. ° ° |
D. ° ° |
如图(5)所示,已知 ,
, 为反比例函数
为反比例函数 图像上的两点,动点
图像上的两点,动点 在
在 正半轴上运动,当线段
正半轴上运动,当线段 与线段
与线段 之差达到最大时,点
之差达到最大时,点 的坐标是( )
的坐标是( )
有一根长 的金属棒,欲将其截成
的金属棒,欲将其截成 根
根 长的小段和
长的小段和 根
根 长的小段,剩余部分作废料处理,若使废料最少,则正整数
长的小段,剩余部分作废料处理,若使废料最少,则正整数 应分别为( )
应分别为( )
某校从参加计算机测试的学生中抽取了60名学生的成绩(40~100分)进行分析,并将其分成了六段后绘制成如图(6)所示的频数分布直方图(其中70~80段因故看不清),若60分以上(含60分)为及格,试根据图中信息来估计这次测试的及格率约为 .
将下列正确的命题的序号填在横线上 .
①若 大于2的正整数,则
大于2的正整数,则 边形的所有外角之和为
边形的所有外角之和为 .
.
②三角形三条中线的交点就是三角形的重心.
③证明两三角形全等的方法有: 及
及 等.
等.
如图(7)所示,已知 点从点(1,0)出发,以每秒1个单位长的速度沿着
点从点(1,0)出发,以每秒1个单位长的速度沿着 轴的正方向运动,经过
轴的正方向运动,经过 秒后,以
秒后,以 、
、 为顶点作菱形
为顶点作菱形 ,使
,使 、
、 点都在第一象限内,且
点都在第一象限内,且 ,又以
,又以 (0,4)为圆心,
(0,4)为圆心, 为半径的圆恰好与
为半径的圆恰好与 所在直线相切,则
所在直线相切,则 .
.
已知甲同学手中藏有三张分别标有数字 的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为
的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为 .
.请你用树形图或列表法列出所有可能的结果.
现制定这样一个游戏规则:若所选出的
 能使得
能使得 有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释
有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释
如图(9)所示(左图为实景侧视图,右图为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架 和
和 (均与水平面垂直),再将集热板安装在
(均与水平面垂直),再将集热板安装在 上.为使集热板吸热率更高,公司规定:
上.为使集热板吸热率更高,公司规定: 与水平面夹角为
与水平面夹角为 ,且在水平线上的射影
,且在水平线上的射影 为
为 .现已测量出屋顶斜面与水平面夹角为
.现已测量出屋顶斜面与水平面夹角为 ,并已知
,并已知 ,
, 。如果安装工人确定支架
。如果安装工人确定支架 高为
高为 ,求支架
,求支架 的高(结果精确到
的高(结果精确到 )?
)?
某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元) 函数解析式;
函数解析式;小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法。
如图(10)所示:等边△ 中,线段
中,线段 为其内角平分线,过
为其内角平分线,过 点的直线
点的直线 于
于 交
交 的延长线于
的延长线于 .
.
请你探究:
 ,是否成立?
,是否成立?请你继续探究:若△
 为任意三角形,线段
为任意三角形,线段 为其内角平分线,请问
为其内角平分线,请问 一定成立吗?并证明你的判断.
一定成立吗?并证明你的判断.
 的倒数是( )
的倒数是( )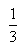
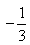
 ,用科学计数法(保留三个有效数字)表示为
,用科学计数法(保留三个有效数字)表示为 ,则
,则 ( )
( )
 的圆心角为120°,半径为2,则图中阴影部分的面积为( )
的圆心角为120°,半径为2,则图中阴影部分的面积为( )

 中,
中, ,
, ,现将其沿
,现将其沿 对折,使得点
对折,使得点 与点
与点 重合,则
重合,则 长为( )
长为( )
 = .
= . 的不等式组
的不等式组 有实数解,则
有实数解,则 的取值范围是 .
的取值范围是 .

 ,其中
,其中
 .
.


 的函数解析式为
的函数解析式为 ,若抛物线
,若抛物线
 ,请证明:
,请证明: ≥
≥ ,并说明
,并说明 为何值时才会有
为何值时才会有 .
. ,设
,设 用含有
用含有 的表达式表示出△
的表达式表示出△ 的面积
的面积 ,并求出
,并求出 的函数解析式。
的函数解析式。 ,则
,则 ,
, 两点间的距离为)
两点间的距离为)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号