[湖北]2012届湖北省随州市四校中考模拟联考数学卷
下列运算正确的是( )
| A.a2+a3=a6 | B.2(a+b)=2a+b | C.(ab)-2=ab-2 | D.a6÷a2=a4 |
我国第六次人口普查显示,全国总人口为1370536875人,将这个总人口数(保留三个有效数字)用科学计数法表示为( )
| A.1.37×109 | B.1.371×109 | C.13.7×108 | D.0.137×1010 |
若x=2是关于x的一元二次方程x2-mx+8=0的一个解,则m的值是( )
| A.6 | B.5 | C.2 | D.-6 |
如图,Rt△ABC中,∠BAC=90°,∠B=60°,△AB′C′可以由△ABC绕点A顺时针旋转90°得到(点B′与点B是对应点,点C′与点C是对应点),连结CC′,则∠CC′B′的度数是( )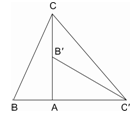
| A.45° | B.30° | C.25° | D.15° |
如图,⊙O是△ABC的外接圆,∠BAC=60°,若⊙O的半径OC为2,则弦BC的长为( )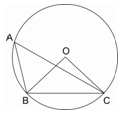
| A.1 | B. |
C.2 | D.2 |
如图,在正五边形ABCDE中,对角线AD、AC与EB分别相交于点M、N;下列结论错误的是( )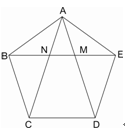
A、四边形EDCN是菱形 B、四边形MNCD是等腰梯形
C、△AEM与△CBN相似 D、△AEN与△EDM全等
甲乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数图象是( )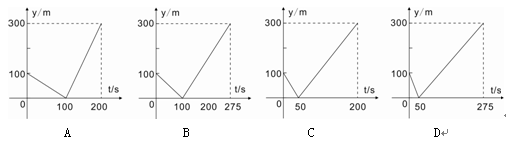
如图,∠ACB=60°,半径为1cm的⊙O切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与AC也相切时,圆心O移动的水平距离是_____cm。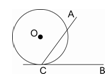
现有30%圆周的一个扇形彩纸片,该扇形的半径是40cm,小红同学为了在“六一”儿童节联欢晚会上表演节目,他打算剪去部分扇形纸片后,利用剩下的纸片制作一个底面半径为10cm的圆锥形纸帽(接缝处不重叠),那么剪去的扇形纸片的圆心角为___。
如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y= 的图象相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连结CF、DE,有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④△DCE≌△CDF,其中正确的结论是______(把你认为正确结论的序号填上。)
的图象相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连结CF、DE,有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④△DCE≌△CDF,其中正确的结论是______(把你认为正确结论的序号填上。)
某中学九年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试,现将项目选择情况及训练后篮
球定时定点投篮测试成绩整理后作出如下统计图表:
| 进球数(个) |
8 |
7 |
6 |
5 |
4 |
3 |
| 人数 |
2 |
1 |
4 |
7 |
8 |
2 |
(1)求选择长跑训练的人数占全班人数的百分比和该班学生的总人数。
(2)求训练后篮球定时定点投篮人均进球数。
(3)根据测试资料,训练后篮球定时定点投篮人均进球数比训练之前人均进行球增加25%。求参加训练之前的人均进球数。
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=DC,连结CF。
(1)求证D是BC的中点。
(2)如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论。
“六一”儿童节,小明与小亮受邀到科技馆担任义务讲解员,他们俩各自独立从A区(时代辉煌)、B区(科学启迪)、C区(智慧之光)、D区(儿童世界)这四个主题展区随机选择一个为参观者服务。
(1)请用列表法或画树状图法说明当天小明与小亮出现在各主题展区担任义务讲解员的所有可能情况(用字母表示)。
(2)求小明和小亮只单独出现在C区(智慧之光)、D区(儿童世界)两个主题展区中担任义务讲解员的概率。
进行防汛期后,某地对河堤进行了加固,该地驻军在河堤加固的工程出色完成了任务,下面是记者与驻军工程指挥官的一段对话:
记者:你们是用了9天完成了4800m长的大坝加固任务的?
指挥官:是的,我们加固600m后,采用新的加固模式,这样每天加固长度是原来的2倍。
通过这段对话,请你求该地驻军原来每天加固的米数。
如图,AB为⊙O的直径,PQ切⊙O于点T,AC⊥PQ于点C,交⊙O于点D。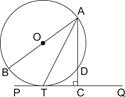
(1)求证:AT平分∠BAC。
(2)若AD=2,TC=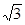 ,求⊙O的半径。
,求⊙O的半径。
如图,河边有一斜坡AB,坡度i=4:3,AB=10m,小明站在坡上的G点处,看见正前方的河里有一只小船C,此时小船C的俯角为30°,若小明的眼睛与地面的距离DG是1.5m,BG=1m,BG平行于CA所在的直线(CA、DC、AB在同一平面内),则CA的长是多少米?(结果精确到0.1m,参考数据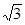 ≈1.7)
≈1.7)
随州购物中心准备采购数量相同的甲、乙两种衬衫,每件以相同的售价x元出售,其中50≤x≤120,甲种衬衫每件进价为30元,当每件定价为50元时,月销售量为120件,每件售价不超过100元时,价格每上涨1元,每件销量减少1件;售价超过100元时,超过100元的部分,每上涨1元,销量减少2件,销售甲种衬衫的月利润为y1(元),销售乙种衬衫的月利润为y2(元),且y2与x的函数关系为y2=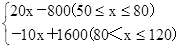 ,销售这两种衬衫的月利润W(元)是y1与y2的和。
,销售这两种衬衫的月利润W(元)是y1与y2的和。
(1)求y1关于x的函数关系式。
(2)求出W关于x的函数关系式。
(3)商场经理如何采购,如何定价,才能使每月获得的总利润W最大?说明理由。
如图所示,直角梯形ABCD中,AD∥BC,∠B=90°,AD=6,BC=8,AB=3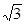 ,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。
,点M是BC的中点,点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动,到达点B后立刻以原速度沿BM返回;点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动,在点P、Q的运动过程中,以PQ为边作等边△EPQ,使它与梯形ABCD在射线BC的同侧,点P、Q同时出发,点P返回到点M时停止运动,点Q也随之停止,设点P、Q运动的时间是t秒(t>0)。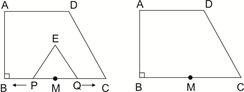
(1)设PQ的长为y,写出y与t之间的函数关系式(写出t的取值范围)。
(2)当BP=1时,求△EPQ与梯形ABCD重叠部分的面积。
(3)随着时间t的变化,线段AD会有一部分被△EPQ覆盖,被覆盖线段的长度在某个时刻会达到最大值,请回答:该最大值能否持续一个时段?若能,直接写出t的取值范围;若不能,请说明理由。
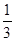 、
、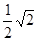 ,sin60°中,无理数的个数为( )
,sin60°中,无理数的个数为( )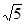 ×
×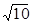 -
-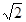 =_____。
=_____。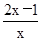 )÷(1-
)÷(1-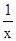 )=_____。
)=_____。 =
= ,DE=4cm,则BC=_____cm。
,DE=4cm,则BC=_____cm。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号