[浙江]2011-2012学年浙江杭州七校高二下期期中理科数学试卷
如图,射线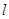 和圆
和圆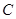 ,当
,当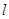 从
从 开始在平面上绕端点
开始在平面上绕端点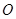 按逆时针方向匀速转动(转动角度不超过
按逆时针方向匀速转动(转动角度不超过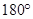 )时,它扫过的圆内阴影部分的面积
)时,它扫过的圆内阴影部分的面积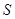 是时间
是时间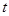 的函数,这个函数的图象大致是( ▲ )
的函数,这个函数的图象大致是( ▲ )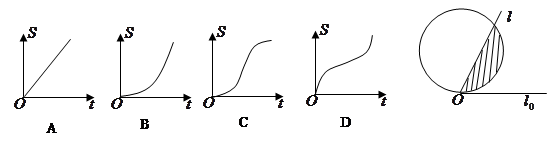
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
已知二次函数 ,且
,且 则不同的二次函数有( ▲ )
则不同的二次函数有( ▲ )
| A.125个 | B.100个 | C.15 个 | D.10个 |
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
篮球队从甲、乙等 名队员中挑选
名队员中挑选 名上场比赛,要求甲、乙中至少有
名上场比赛,要求甲、乙中至少有 人参加,则下列选派方法种数表示不正确的是( ▲ )
人参加,则下列选派方法种数表示不正确的是( ▲ )
A. |
B. |
C. |
D. |
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
已知结论:“在正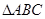 中,
中,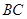 中点为
中点为 ,若
,若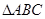 内一点
内一点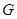 到各边的距离都相等,则
到各边的距离都相等,则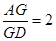 ”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体
”.若把该结论推广到空间,则有结论:“在棱长都相等的四面体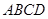 中,若
中,若 的中心为
的中心为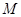 ,四面体内部一点
,四面体内部一点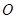 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则 ( ▲ )
( ▲ )
| A.1 | B.2 | C.3 | D.4 |
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
下图都是由边长为1的正方体叠成的图形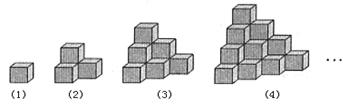
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位,第(4)个图形的表面积是60个平方单位.依此规律,则第(8)个图形的表面积是 ▲ 个平方单位.
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
将四个女生和三个男生随机排成一排,然后从左至右依次给他们编号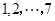 ,则男生的编号之和小于女生编号之和的排法有 ▲ 种.(请用数字作答)
,则男生的编号之和小于女生编号之和的排法有 ▲ 种.(请用数字作答)
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
对于函数 ,若存在区间
,若存在区间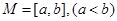 ,使得
,使得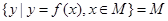 ,则称区间
,则称区间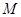 为函数
为函数 的一个“稳定区间”.现有四个函数:
的一个“稳定区间”.现有四个函数:
①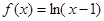 ②
②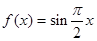 ③
③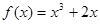 ④
④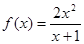 .
.
其中存在“稳定区间”的函数有 ▲
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
来源:2011-2012学年浙江杭州七校高二下期期中理科数学试卷
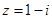 ,则
,则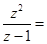 ( ▲ )
( ▲ )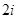
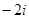
 ,
, ,
, ,则
,则 的大小关系是( ▲ )
的大小关系是( ▲ )



 在
在 上( ▲ )
上( ▲ ) 的展开式中,
的展开式中, 的幂指数是整数的项共有( ▲ )
的幂指数是整数的项共有( ▲ ) 项
项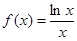 ,若方程
,若方程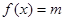 存在两个不同的实数解,则实数
存在两个不同的实数解,则实数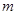 的取值范围为( ▲ )
的取值范围为( ▲ )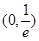
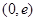
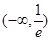

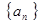 定义如下:
定义如下: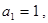
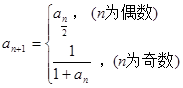 , 则前
, 则前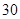 项中使
项中使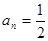 的项的个数是( ▲ )
的项的个数是( ▲ )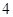
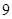
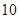
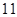
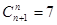 ,那么
,那么 = ▲
= ▲ 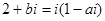 ,其中
,其中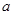 、
、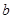
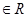 ,
,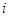 是虚数单位,则
是虚数单位,则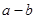 = ▲
= ▲ 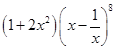 的展开式中常数项为 ▲ (请用数字作答)
的展开式中常数项为 ▲ (请用数字作答)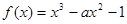 在
在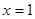 处的切线经过原点
处的切线经过原点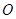 ,则函数
,则函数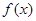 的极小值为 ▲
的极小值为 ▲  ,且
,且 .
. 的值;
的值;  的值.
的值. .
. 在区间
在区间 上的最大值;
上的最大值; 在区间
在区间 上存在递减区间,求实数m的取值范围.
上存在递减区间,求实数m的取值范围. .(
.( )
) 在区间
在区间 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围; 上,函数
上,函数 下方,求
下方,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号