[北京]2012届北京石景山区中考模拟数学卷

－的倒数是         ；－3－（－5）=          。

分解因式：－x³＋2x²－x=              ;计算：=         .

纳米（nm）是一种长度单位，1nm=10^－9m,已知某种植物花粉的直径约为4330nm,那么用科学计数法表示花粉的直径为               m.

如图1所示，⊙O的两条切线PA和PB相交于点P，与⊙O相切于A、B两点，C是⊙O上的一点，若∠P=70⁰，则∠ACB=         。

函数y=中，自变量x的取值范围是             。

为了了解学生使用零花钱的情况，小军随机的抽查了他们班的30名学生，结果如下表：

这些同学每天使用零花钱的众数是          ，中位数是         。

若a，b是实数，式子和|a—2|互为相反数，则（a+b）²⁰¹¹=       .

某种药品原价为100元，经过连续两次的降价后，价格变为64元，如果每次降价的百分率是一样的，那么每次降价后的百分率是              .

如图2，四边形ABCD是平行四边形，E是CD延长线上的任意一点，连接BE交AD于点O，如果△ABO≌△DEO，则需要添加的条件是               。（只需一个即可，图中不能添加任何点或线）

若点A（2，a）关于x轴的对称点是B（b，－3）则ab的值是         .

如图3，△ABC是一块锐角三角形的材料，边BC=120mm，高AD=80mm，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是    mm.

用黑白两种正六边形地面瓷砖按如图4所示规律拼成若干图案，则第n个图案中有白色地面瓷砖       块。

第1个    第2个      第3个

某同学手里拿着长为3和2的两个木棍，想要装一个木棍，用它们围成一个三角形，那么他所找的这根木棍长满足条件的整数解是 （    ）

如图5,是一个水管的三叉接头，它的左视图是（ ）

图5                     A        B         C              D

在 3.14，，π和这四个实数中，无理数是（ ）

A．3.14和

B．π和

C．和

D．π和

将y=2x²的函数图象向左平移2个单位长度后，得到的函数解析式是（  ）

关于x的一元二次方程x²+4x+k=0有实数解，则k的取值范围是（  ）

将y=2x²的函数图象向左平移2个单位长度后，得到的函数解析式是（  ）

一次函数y=－2x+1和反比例函数y=的大致图象是（  ）

A                B                   C              D

如图6，天平右盘中的每个砝码的质量都是1克，则物体A的质量m克的取值范围表示在数轴上为（  ）

计算：

请你先化简分式

学校在艺术周上，要求学生制作一个精美的轴对称图形，请你用所给出的几何图形：○○△△    （两个圆，两个等边三角形，两条线段）为构件，构思一个独特，有意义的轴对称图形，并写上一句简要的解说词。

某学校九年级的学生去旅游，在风景区看到一棵古松，不知这棵古松有多高，下面是他们的一段对话：
甲：我站在此处看树顶仰角为45°。
乙：我站在此处看树顶仰角为30°。
甲：我们的身高都是1.5m。
乙：我们相距20m。
请你根据两位同学的对话，参考图7计算这棵古松的高度。（参考数据≈1.414，≈1.732，结果保留两位小数）。

已知：如图8，AB是⊙O的直径，AC是弦，直线EF是过点C的⊙O的切线，AD⊥EF于点D.
求证：∠BAC=∠CAD
若∠B=30°，AB=12，求的长.

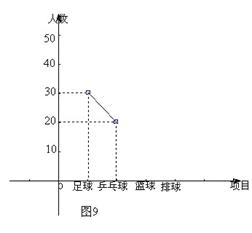
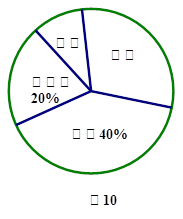
学校为了响应国家阳光体育活动，选派部分学生参加足球、乒乓球、篮球、排球队集训.根据参加项目制成如下两幅不完整的统计图（如图9和如图10，要求每位同学只能选择一种自己喜欢的球类，图中用足球、乒乓球、篮球、排球代表喜欢这四种球类某种球类的学生人数）
请你根据图中提供的信息解答下列问题：
参加篮球对的有       人，参加足球对的人数占全部参加人数的     %.
喜欢排球队的人数在扇形统计图中所占的圆心角是多少度？并补全频数分布折线统计图.
若足球对只剩一个集训名额，学生小明和小虎都想参加足球队，决定采用随机摸球的方式确定参加权，具体规则如下：一个不透明的袋子中装着标有数字1、2、3、4的四个完全相同的小球，小明随机地从四个小球中摸出一球然后放回，小虎再随机地摸出一球，若小明摸出的小球标有数字比小虎摸出的小球标有的数字大，则小明参加，否则小虎参加，试分析这种规则对双方是否公平？

认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题.
探究如图11-1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，通过分析发现∠BOC=90°+,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线

如图11-2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由.
如图11-3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（只写结论，不需证明）
结论：                                                           .

已知一元二次方程x²－4x＋3=0的两根是m，n且m＜n.如图12，若抛物线y=-x²+bx
+c的图像经过点A（m，0）、B（0，n）.
求抛物线的解析式.
若（1）中的抛物线与x轴的另一个交点为C.根据图像回答，当x取何值时，抛物线的图像在直线BC的上方？
点P在线段OC上，作PE⊥x轴与抛物线交与点E，若直线BC将△CPE的面积分成相等的两部分，求点P的坐标.