[福建]福建省仙游县2011-2012学年第二教研区九年级考试数学卷
天气预报明天枫亭地区下雨的概率为70%,则下列理解正确的是( )
| A.明天30%的地区会下雨 | B.明天30%的时间会下雨 |
| C.明天出行不带雨伞一定会被淋湿 | D.明天出行不带雨伞被淋湿的可能性很大 |
如图所示,△ABC之外任取一点O,连AO、BO、CO,并取它们的中点D、E、F得到△DEF,下列说法中正确的个数是( )
①△ABC与△DEF是位似图形;
②△ABC与△DEF是相似形;
③△ABC与△DEF的周长之比为2:1;
④△ABC与△DEF面积比为4:1;
A. 1个 B. 2个 C. 3个 D. 4个
如图所示,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB等于( )
| A.4.5米 | B.6米 |
| C.7.5米 | D.8米 |
为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间等有标记的鱼完全混合于鱼群中以后,再捕捞150条,若其中有标记的鱼有10条,则估计池塘里有鱼 条.
(8分) 现有9个相同的小正三角形拼成的大正三角形,将其部分涂黑.如图(1),(2)所示.



图(1) 图(2) 图(3) 图(4)
观察图(1),图(2)中涂黑部分构成的图案.它们具有如下特征:①都是轴对称图形②涂黑部分都是三个小正三角形.
请在图(3),图(4)内分别设计一个新图案,使图案具有上述两个特征
(10分) 某商场销售一批名牌衬衫:平均每天可售出20件,每件盈利40元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价促销措施,经市场调查发现:如果每件衬衫降价1元,那么平均每天就可多售出2件。
(1)求出商场盈利与每件衬衫降价之间的函数关系式;(5分)
(2)若每天盈利达1200元,那么每件衬衫应降价多少元?(5分)
(10分) 如图,以Rt△ABC的直角边AB为直径的半圆O,与斜边AC交于D,E是BC边上的中点,连结DE. 

(1)DE与半圆O相切吗?若相切,请给出证明;若不相切,请说明理由;( 5分)
(2)若AD、AB的长是方程x2-10x+24=0的两个根,求直角边BC的长。(5分)
.(12分)如图1:⊙O的直径为AB,过半径OA的中点G作弦CE⊥AB,在 上取一点D,分别作直线CD、ED交直线AB于点F、M。
上取一点D,分别作直线CD、ED交直线AB于点F、M。
(1)求∠COA和∠FDM的度数;(3分)
(2)求证:△FDM∽△COM;(4分)
(3)如图2:若将垂足G改取为半径OB上任意一点,点D改取在 上,仍作直线CD、ED,分别交直线AB于点F、M,试判断:此时是否仍有△FDM∽△COM?证明你的结论。(5分)
上,仍作直线CD、ED,分别交直线AB于点F、M,试判断:此时是否仍有△FDM∽△COM?证明你的结论。(5分)














 与
与 轴没有交点,其中R、r分别为⊙
轴没有交点,其中R、r分别为⊙ ,⊙
,⊙ 的半径,d为两圆的圆心距,则⊙
的半径,d为两圆的圆心距,则⊙ 时,二次根式
时,二次根式 无意义.
无意义.
 的方程
的方程 有两个相等的实根,
有两个相等的实根, 的对称轴是__________
的对称轴是__________ ,b=
,b= ,则a与b之间的大小关系是________
,则a与b之间的大小关系是________

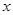 的一元二次方程
的一元二次方程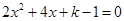 有实数根,
有实数根, 为正整数.
为正整数. 是方程
是方程 的两个实数根,且
的两个实数根,且 ,抛物线
,抛物线 的图像经过点A(
的图像经过点A( )、B(
)、B( ).
). 轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(5分)
轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;(5分)  粤公网安备 44130202000953号
粤公网安备 44130202000953号