[浙江]2011年桐乡市五校八年级上学期期中考试数学卷
一架2.5米长的梯子斜靠在一竖直的墙上,这时梯子的顶端距墙脚2.4米。那么梯足离墙脚的距离是( ▲ )
| A.0.7米 | B.0.9米 | C.1.5米 | D.2.4米 |
下面的图形中,不是轴对称图形的是( ▲ )
| A.有两个角相等的三角形; |
| B.有一个内角是40°,另一个内角是100°的三角形; |
| C.三个内角的度数比是2:3:4的三角形; |
| D.三个内角的度数比是1:1:2的三角形。 |
如图,AD是△ABC中∠BAC的平分线,DE⊥AB交AB于点E,DF⊥AC交AC于点F。若S△ABC=7,DE=2,AB=4,则AC=( )
| A.3 | B.4 | C.5 | D.6 |
如图△ABC中,∠ABC与∠ACB的平分线交于点F,过点F作DE∥BC交AB于点D交AC于点E,那么下列结论中正确的是 ( ▲ )
①△BOF和△CEF都是等腰三角形
②DE=BD+CE
③△ADE的周长等于AB和AC的和
④BF="CF "
| A.①②③④ | B.①②③ | C.①② | D.① |
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上, AE与CD交于点G,AC与BD交于点F,连接FG,则下列结论要:①AE=BD;②AG=BF;③ 是等边三角形;④FG∥BE,其中正确结论的个数( ▲ )
是等边三角形;④FG∥BE,其中正确结论的个数( ▲ )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,已知 与
与 是两个全等的直角三角形,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点
是两个全等的直角三角形,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点 在同一条直线上,且点
在同一条直线上,且点 与点
与点 重合,将图(1)中的
重合,将图(1)中的 绕点
绕点 顺时针方向旋转到图(2)的位置,点
顺时针方向旋转到图(2)的位置,点 在
在 边上,
边上, 交
交 于点
于点 ,则∠ECG= ▲ 。
,则∠ECG= ▲ 。
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整。
解:∵EF∥AD ( 已知 )
∴∠2=_______( )
又∵∠1=∠2 ( 已知 )
∴∠1=∠3
∴AB∥_______( )
∴∠BAC+_____=180°
又∵∠BAC=70°
∴∠AGD=_______
直线a经过正方形ABCD的顶点A,分别过顶点B、D作BE⊥a于点E、DF⊥a于点F,若BE=4,DF=3,求EF的长及正方形的面积。(注:正方形的四边都相等,四个角都是直角)
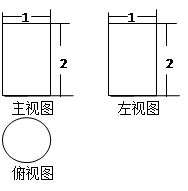
棱长为1cm的小正方形组成如图所示的零件模型,要将模型表面油漆成紫色(黏合的部分及地面接触部分不油漆)。
求:模型的涂漆面积;
若模型表面涂漆加工费为5元每平方厘米,
那么这个模型的总加工费是多少元?

 ,小明课间把老师的三角板的直角顶点放在
,小明课间把老师的三角板的直角顶点放在 上,已知
上,已知 ,则
,则 的度数为( ▲ )
的度数为( ▲ )






 ,则此三角形是 ( ▲ )
,则此三角形是 ( ▲ )
 ,
,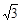 ,
,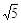 ; ② 1,1,2;③5,12,13 ;④6,7,8 ⑤3,4,5
; ② 1,1,2;③5,12,13 ;④6,7,8 ⑤3,4,5

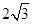 ,在直线a上有一动点C,当△ABC为等腰三角形时,则线段AC的长___▲_____。
,在直线a上有一动点C,当△ABC为等腰三角形时,则线段AC的长___▲_____。




 粤公网安备 44130202000953号
粤公网安备 44130202000953号