2017年山东省青岛市中考数学试卷
小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法中错误的

A.众数是6吨B.平均数是5吨C.中位数是5吨D.方差是
一次函数 的图象经过 , 两点, 为反比例函数 图象上一动点, 为坐标原点,过点 作 轴的垂线,垂足为 ,则 的面积为
A.2B.4C.8D.不确定
小华和小军做摸球游戏: 袋装有编号为1,2,3的三个小球, 袋装有编号为4,5,6的三个小球,两袋中的所有小球除编号外都相同.从两个袋子中分别随机摸出一个小球,若 袋摸出小球的编号与 袋摸出小球的编号之差为偶数,则小华胜,否则小军胜.这个游戏对双方公平吗?请说明理由.
某中学开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的统计图,已知“查资料”的人数是40人.

请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的圆心角度数是 度;
(2)补全条形统计图;
(3)该校共有学生1200人,估计每周使用手机时间在2小时以上(不含2小时)的人数.
如图, 地在 地的正东方向,因有大山阻隔,由 地到 地需绕行 地.已知 地位于 地北偏东 方向,距离 地 , 地位于 地南偏东 方向.若打通穿山隧道,建成两地直达高铁,求 地到 地之间高铁线路的长.(结果保留整数)
(参考数据: , , ,

, 两地相距 ,甲、乙两人从两地出发相向而行,甲先出发.图中 , 表示两人离 地的距离 与时间 的关系,请结合图象解答下列问题:
(1)表示乙离 地的距离与时间关系的图象是 (填 或 ;甲的速度是 ,乙的速度是 ;
(2)甲出发多少小时两人恰好相距 ?

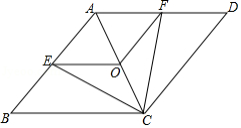
已知:如图,在菱形 中,点 , , 分别为 , , 的中点,连接 , , , .
(1)求证: ;
(2)当 与 满足什么关系时,四边形 是正方形?请说明理由.
青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 .下表是去年该酒店豪华间某两天的相关记录:
淡季 |
旺季 |
|
未入住房间数 |
10 |
0 |
日总收入(元 |
24000 |
40000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
探究一:求不等式 的解集
(1)探究 的几何意义
如图①,在以 为原点的数轴上,设点 对应的数是 ,由绝对值的定义可知,点 与点 的距离为 ,可记为 .将线段 向右平移1个单位得到线段 ,此时点 对应的数是 ,点 对应的数是1.因为 ,所以 .因此, 的几何意义可以理解为数轴上 所对应的点 与1所对应的点 之间的距离 .
(2)求方程 的解
因为数轴上3和 所对应的点与1所对应的点之间的距离都为2,所以方程的解为3, .
(3)求不等式 的解集
因为 表示数轴上 所对应的点与1所对应的点之间的距离,所以求不等式解集就转化为求这个距离小于2的点对应的数 的范围.
请在图②的数轴上表示 的解集,并写出这个解集.
探究二:探究 的几何意义
(1)探究 的几何意义
如图③,在直角坐标系中,设点 的坐标为 ,过 作 轴于 ,作 轴于 ,则 点坐标为 , 点坐标为 , , ,在 中, ,则 ,因此, 的几何意义可以理解为点 与点 之间的距离 .
(2)探究 的几何意义
如图④,在直角坐标系中,设点 的坐标为 ,由探究二(1)可知, ,将线段 先向右平移1个单位,再向上平移5个单位,得到线段 ,此时点 的坐标为 ,点 的坐标为 ,因为 ,所以 ,因此 的几何意义可以理解为点 与点 之间的距离 .
(3)探究 的几何意义
请仿照探究二(2)的方法,在图⑤中画出图形,并写出探究过程.
(4) 的几何意义可以理解为: .
拓展应用:
(1) 的几何意义可以理解为:点 与点 的距离和点 与点 (填写坐标)的距离之和.
(2) 的最小值为 (直接写出结果)

已知: 和矩形 如图①摆放(点 与点 重合),点 , , 在同一直线上, , , .如图②, 从图①的位置出发,沿 方向匀速运动,速度为 , 与 交于点 ;同时,点 从点 出发,沿 方向匀速运动,速度为 .过点 作 ,垂足为 ,交 于点 ,连接 , ,当点 停止运动时, 也停止运动.设运动时间为 ,解答下列问题:
(1)当 为何值时, ?
(2)设五边形 的面积为 ,求 与 之间的函数关系式;
(3)在运动过程中,是否存在某一时刻 ,使 ?若存在,求出 的值;若不存在,请说明理由.
(4)在运动过程中,是否存在某一时刻 ,使点 在线段 的垂直平分线上?若存在,求出 的值;若不存在,请说明理由.

 B.
B. C.
C. D.
D.






 粤公网安备 44130202000953号
粤公网安备 44130202000953号