2016年山东省烟台市中考数学试卷
某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 |
乙 |
丙 |
|
平均数 |
7.9 |
7.9 |
8.0 |
方差 |
3.29 |
0.49 |
1.8 |
根据以上图表信息,参赛选手应选

A.甲B.乙C.丙D.丁
如图,在平面直角坐标系中,正方形 与正方形 是以原点 为位似中心的位似图形,且相似比为 ,点 , , 在 轴上,若正方形 的边长为6,则 点坐标为

A. B. C. D.
如图, 的斜边 与量角器的直径恰好重合, 点与0刻度线的一端重合, ,射线 绕点 转动,与量角器外沿交于点 ,若射线 将 分割出以 为边的等腰三角形,则点 在量角器上对应的度数是
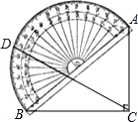
A. B. C. 或 D. 或
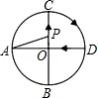
如图, 的半径为1, , 是 的两条互相垂直的直径,点 从点 出发 点与 点不重合),沿 的路线运动,设 , ,那么 与 之间的关系图象大致是
A.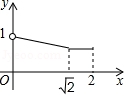 B.
B.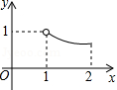
C.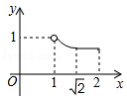 D.
D.
如图, 为数轴原点, , 两点分别对应 ,3,作腰长为4的等腰 ,连接 ,以 为圆心, 长为半径画弧交数轴于点 ,则点 对应的实数为 .

如图, 为半圆内一点, 为圆心,直径 长为 , , ,将 绕圆心 逆时针旋转至△ ,点 在 上,则边 扫过区域(图中阴影部分)的面积为 .(结果保留

如图,在正方形纸片 中, , , 是线段 的六等分点,若把该正方形纸片卷成一个圆柱,使点 与点 重合,此时,底面圆的直径为 ,则圆柱上 , 两点间的距离是 .

网上购物已经成为人们常用的一种购物方式,售后评价特别引人关注,消费者在网店购买某种商品后,对其有“好评”、“中评”、“差评”三种评价,假设这三种评价是等可能的.

(1)小明对一家网店销售某种商品显示的评价信息进行了统计,并列出了两幅不完整的统计图.
利用图中所提供的信息解决以下问题:
①小明一共统计了 个评价;
②请将图1补充完整;
③图2中“差评”所占的百分比是 ;
(2)若甲、乙两名消费者在该网店购买了同一商品,请你用列表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率.
由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
|
甲 |
乙 |
原料成本 |
12 |
8 |
销售单价 |
18 |
12 |
生产提成 |
1 |
0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本 生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润 销售收入 投入总成本)
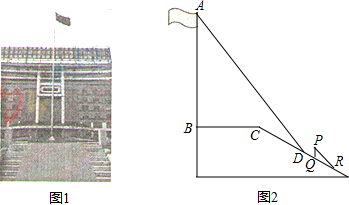
某中学广场上有旗杆如图1所示,在学习解直角三角形以后,数学兴趣小组测量了旗杆的高度.如图2,某一时刻,旗杆 的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长 为4米,落在斜坡上的影长 为3米, ,同一时刻,光线与水平面的夹角为 ,1米的竖立标杆 在斜坡上的影长 为2米,求旗杆的高度(结果精确到0.1米).(参考数据: , ,
如图, 内接于 , 为 的直径, 是 的切线, 为切点, ,垂足为 ,交 于 ,连接 .
(1)求证: 平分 ;
(2)若 的半径为1, ,求 及 的长.

(探究证明)
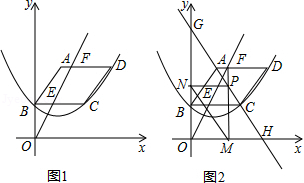
(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
如图1,矩形 中, , 分别交 , 于点 , , 分别交 , 于点 , .求证: ;
(结论应用)
(2)如图2,在满足(1)的条件下,又 ,点 , 分别在边 , 上,若 ,则 的值为 ;
(联系拓展)
(3)如图3,四边形 中, , , , ,点 , 分别在边 , 上,求 的值.

 B.
B. C.
C. D.
D.

 B.
B. C.
C. D.
D.









 粤公网安备 44130202000953号
粤公网安备 44130202000953号