2017年贵州省黔西南州中考数学试卷
已知甲、乙两同学1分钟跳绳的平均数相同,若甲同学1分钟跳绳成绩的方差 ,乙同学1分钟跳绳成绩的方差 ,则
A.甲的成绩比乙的成绩更稳定
B.乙的成绩比甲的成绩更稳定
C.甲、乙两人的成绩一样稳定
D.甲、乙两人的成绩稳定性不能比较
一个不透明的袋中共有20个球,它们除颜色不同外,其余均相同,其中:8个白球,5个黄球,5个绿球,2个红球,则任意摸出一个球是红球的概率是
A. B. C. D.
如图,点 是反比例函数 上的一个动点,连接 ,过点 作 ,并且使 ,连接 ,当点 在反比例函数图象上移动时,点 也在某一反比例函数 图象上移动,则 的值为

A. B.4C. D.2
人工智能 ,因在人机大战中大胜韩国围棋手李世石和我国选手柯洁而声名显赫,它具有自我对弈的学习能力,决战前已做了两千万局的训练(等同于一个近千年的训练量)此处“两千万”用科学记数法表示为 (精确到百万位).
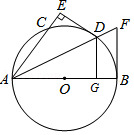
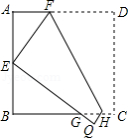
如图,已知 为 直径, 是 的中点, 交 的延长线于 , 的切线交 的延长线于 .
(1)求证:直线 与 相切;
(2)已知 且 , 的半径为5,求 的值.
今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用 、 、 、 表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题:
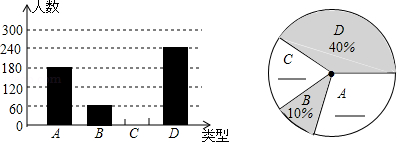
(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃 粽的人数.
(4)若有外型完全相同的 、 、 、 粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是 粽的概率.
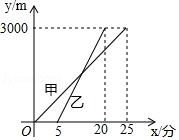
赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点 驶向终点 ,在整个行程中,龙舟离开起点的距离 (米 与时间 (分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点 与终点 之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的 与 函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?
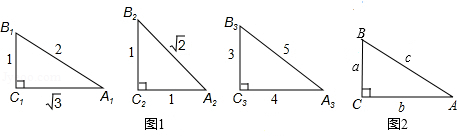
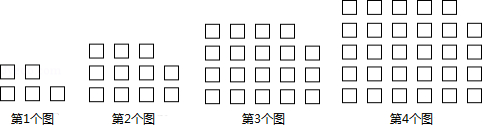
把 记作 ,根据图1和图2完成下列各题.
(1) , , ;
(2)观察上述等式猜想:在 中, ,总有 ;
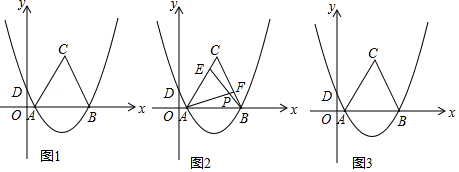
(3)如图2,在 中证明(2)题中的猜想:
(4)已知在 中, ,且 ,求 .
 B.
B. C.
C. D.
D.



 粤公网安备 44130202000953号
粤公网安备 44130202000953号