2017年贵州省铜仁市中考数学试卷
如图, 沿着 方向平移得到△ ,点 是直线 上任意一点,若 ,△ 的面积分别为 , ,则下列关系正确的是
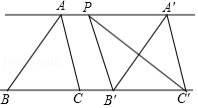
A. B. C. D.
来源:2017年贵州省铜仁市中考数学试卷
观察下列关于自然数的式子:
①
②
③
根据上述规律,则第2017个式子的值是
A.8064B.8065C.8066D.8067
来源:2017年贵州省铜仁市中考数学试卷
如图,身高为1.8米的某学生想测量学校旗杆的高度,当他站在 处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得 米, 米,则旗杆 的高度是 米.

来源:2017年贵州省铜仁市中考数学试卷
某校为了了解九年级九年级学生体育测试情况,随机抽查了部分学生的体育测试成绩的样本,按 , , 等:成绩大于或等于80分; 等:成绩大于或等于60分且小于80分; 等:成绩小于60分)三个等级进行统计,并将统计结果绘制成如下的统计图,请你结合图中所给的信息解答下列问题:
(1)请把条形统计图补充完整;
(2)扇形统计图中 等所在的扇形的圆心角等于 度;
(3)若九年级有1000名学生,请你用此样本估计体育测试在60分以上(包括60分)的学生人数.

来源:2017年贵州省铜仁市中考数学试卷
某商店以20元 千克的单价新进一批商品,经调查发现,在一段时间内,销售量 (千克)与销售单价 (元 千克)之间为一次函数关系,如图所示.
(1)求 与 的函数表达式;
(2)要使销售利润达到800元,销售单价应定为每千克多少元?

来源:2017年贵州省铜仁市中考数学试卷
如图,已知在 中, ,以 为直径的 与 交于点 ,点 是 的中点,连接 , .
(1)若 ,求 ;
(2)求证: 是 的切线.
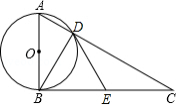
来源:2017年贵州省铜仁市中考数学试卷









 粤公网安备 44130202000953号
粤公网安备 44130202000953号