2016年福建省莆田市中考数学试卷
规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为 的是
的是

A.正三角形B.正方形C.正六边形D.正十边形
如图, 在平面直角坐标系中, 点 ,在
,在 轴上任取一点
轴上任取一点 ,完成以下作图步骤:
,完成以下作图步骤:
①连接 . 作线段
. 作线段 的垂直平分线
的垂直平分线 ,过点
,过点 作
作 轴的垂线
轴的垂线 ,记
,记 ,
, 的交点为
的交点为 ;
;
②在 轴上多次改变点
轴上多次改变点 的位置, 用①的方法得到相应的点
的位置, 用①的方法得到相应的点 ,把这些点用平滑的曲线顺次连接起来, 得到的曲线是
,把这些点用平滑的曲线顺次连接起来, 得到的曲线是


A . 直线B . 抛物线C . 双曲线D . 双曲线的一支
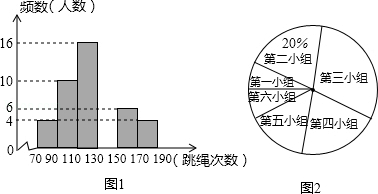
在大课间活动中,同学们积极参加体育锻炼,小红在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,估计该校学生“一分钟跳绳”成绩优秀的人数为 人.
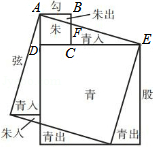
魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中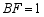 ,
,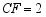 ,则
,则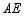 的长为 .
的长为 .
小梅家的阳台上放置了一个晒衣架如图1,图2是晒衣架的侧面示意图, ,
,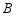 两点立于地面,将晒衣架稳固张开,测得张角
两点立于地面,将晒衣架稳固张开,测得张角 ,立杆
,立杆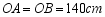 ,小梅的连衣裙穿在衣架后的总长度为
,小梅的连衣裙穿在衣架后的总长度为 ,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据:
,问将这件连衣裙垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由(参考数据: ,
, ,
,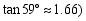

在一次数学文化课题活动中,把一副数学文化创意扑克牌中的4张扑克牌(如图所示)洗匀后正面向下放在桌面上,从中随机抽取2张牌,请你用列表或画树状图的方法,求抽取的2张牌的数字之和为偶数的概率.

甲车从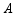 地驶往
地驶往 地,同时乙车从
地,同时乙车从 地驶往
地驶往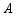 地,两车相向而行,匀速行驶,甲车距
地,两车相向而行,匀速行驶,甲车距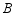 地的距离
地的距离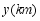 与行驶时间
与行驶时间 之间的函数关系如图所示,乙车的速度是
之间的函数关系如图所示,乙车的速度是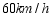
(1)求甲车的速度;
(2)当甲乙两车相遇后,乙车速度变为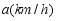 ,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求
,并保持匀速行驶,甲车速度保持不变,结果乙车比甲车晚38分钟到达终点,求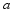 的值.
的值.

如图,在 中,
中, ,对角线
,对角线 ,
, 相交于点
相交于点 ,以
,以 为直径的
为直径的 分别交
分别交 ,
, 于点
于点 ,
, ,连接
,连接 并延长交
并延长交 于点
于点 .
.
(1)求证: 是
是 的切线;
的切线;
(2)求证: .
.

如图,反比例函数
的图象与直线 交于点
交于点 ,
, ,其两边分别与两坐标轴的正半轴交于点
,其两边分别与两坐标轴的正半轴交于点 ,
, ,四边形
,四边形 的面积为6.
的面积为6.
(1)求 的值;
的值;
(2)点 在反比例函数
的图象上,若点
在反比例函数
的图象上,若点 的横坐标为3,
的横坐标为3, ,其两边分别与
,其两边分别与 轴的正半轴,直线
轴的正半轴,直线 交于点
交于点 ,
, ,问是否存在点
,问是否存在点 ,使得
,使得 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形, 中,设
中,设 ,
, ,
, ,各边上的高分别记为
,各边上的高分别记为 ,
, ,
, ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为 ,
, ,
,
(1)模拟探究:如图,正方形 为
为 的
的 边上的内接正方形,求证:
;
边上的内接正方形,求证:
;
(2)特殊应用:若 ,
, ,求
的值;
,求
的值;
(3)拓展延伸:若 为锐角三角形,
为锐角三角形, ,请判断
,请判断 与
与 的大小,并说明理由.
的大小,并说明理由.





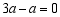 B.
B.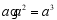 C.
C.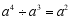 D.
D.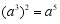
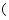
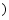



 B.
B. C.
C. D.
D.
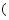
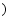
 是
是 的平分线,点
的平分线,点 ,
, 分别在角的两边
分别在角的两边 ,
, 上,添加下列条件,不能判定
上,添加下列条件,不能判定 的选项是
的选项是


 ,
,
 C.
C. D.
D.
 的一元二次方程
的一元二次方程 的根的情况是
的根的情况是

 中,
中, ,
, ,将
,将 折叠,使点
折叠,使点 落在
落在 边上的点
边上的点 处,
处, 为折痕,若
为折痕,若 ,则
,则 的值为
的值为


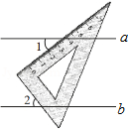
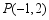 向右平移3个单位长度得到的点的坐标是
向右平移3个单位长度得到的点的坐标是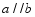 ,一块直角三角板如图所示放置,若
,一块直角三角板如图所示放置,若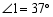 ,则
,则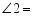
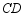 为
为 的弦,直径
的弦,直径 为4,
为4,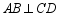 于
于 ,
,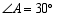 ,则
,则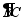 的长为
的长为 .
.
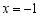 .
. ,与
,与 轴的正半轴交于点
轴的正半轴交于点 .
. 上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式;
上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的解析式; 上的点
上的点 变为
变为 ,
, ,变换后得到的抛物线记作
,变换后得到的抛物线记作 ,抛物线
,抛物线 的顶点为
的顶点为 ,点
,点 在抛物线
在抛物线 上,满足
上,满足 ,且
,且 .
. 时,求
时,求 的值;
的值; 时,请直接写出
时,请直接写出 的值,不必说明理由.
的值,不必说明理由.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号