2020年广东省中考数学试卷
如图,在正方形 中, ,点 , 分别在边 , 上, .若将四边形 沿 折叠,点 恰好落在 边上,则 的长度为

| A. |
1 |
B. |
|
C. |
|
D. |
2 |
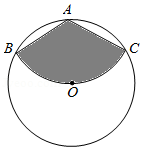
如图,在菱形 中, ,取大于 的长为半径,分别以点 , 为圆心作弧相交于两点,过此两点的直线交 边于点 (作图痕迹如图所示),连接 , .则 的度数为 .

有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .

某中学开展主题为"垃圾分类知多少"的调查活动,调查问卷设置了"非常了解"、"比较了解"、"基本了解"、"不太了解"四个等级,要求每名学生选且只能选其中一个等级,随机抽取了120名学生的有效问卷,数据整理如下:
等级 |
非常了解 |
比较了解 |
基本了解 |
不太了解 |
人数(人 |
24 |
72 |
18 |
|
(1)求 的值;
(2)若该校有学生1800人,请根据抽样调查结果估算该校"非常了解"和"比较了解"垃圾分类知识的学生共有多少人?
已知关于 , 的方程组 与 的解相同.
(1)求 , 的值;
(2)若一个三角形的一条边的长为 ,另外两条边的长是关于 的方程 的解.试判断该三角形的形状,并说明理由.
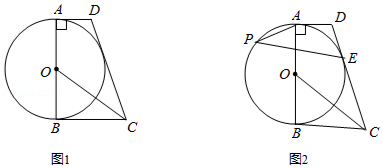
如图1,在四边形 中, , , 是 的直径, 平分 .
(1)求证:直线 与 相切;
(2)如图2,记(1)中的切点为 , 为优弧 上一点, , .求 的值.
某社区拟建 , 两类摊位以搞活"地摊经济",每个 类摊位的占地面积比每个 类摊位的占地面积多2平方米.建 类摊位每平方米的费用为40元,建 类摊位每平方米的费用为30元.用60平方米建 类摊位的个数恰好是用同样面积建 类摊位个数的 .
(1)求每个 , 类摊位占地面积各为多少平方米?
(2)该社区拟建 , 两类摊位共90个,且 类摊位的数量不少于 类摊位数量的3倍.求建造这90个摊位的最大费用.
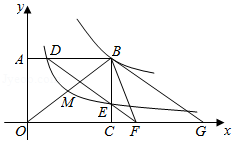
如图,点 是反比例函数 图象上一点,过点 分别向坐标轴作垂线,垂足为 , .反比例函数 的图象经过 的中点 ,与 , 分别相交于点 , .连接 并延长交 轴于点 ,点 与点 关于点 对称,连接 , .
(1)填空: ;
(2)求 的面积;
(3)求证:四边形 为平行四边形.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号