2019年山东省烟台市中考数学试卷
如图所示的几何体是由9个大小相同的小正方体组成的,将小正方体①移走后,所得几何体的三视图没有发生变化的是

| A. |
主视图和左视图 |
B. |
主视图和俯视图 |
| C. |
左视图和俯视图 |
D. |
主视图、左视图、俯视图 |
某种计算机完成一次基本运算的时间约为1纳秒 ,已知1纳秒 000 001秒,该计算机完成15次基本运算,所用时间用科学记数法表示为
| A. |
秒 |
B. |
秒 |
C. |
秒 |
D. |
秒 |
当 时,关于 的一元二次方程 的根的情况为
| A. |
有两个不相等的实数根 |
B. |
有两个相等的实数根 |
| C. |
没有实数根 |
D. |
无法确定 |
某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差 .后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是
| A. |
平均分不变,方差变大 |
B. |
平均分不变,方差变小 |
| C. |
平均分和方差都不变 |
D. |
平均分和方差都改变 |
已知 ,以 为圆心,以任意长为半径作弧,交 , 于点 , ,分别以点 , 为圆心,以大于 的长度为半径作弧,两弧在 内交于点 ,以 为边作 ,则 的度数为
| A. |
|
B. |
|
C. |
或 |
D. |
或 |
南宋数学家杨辉在其著作《详解九章算法》中揭示了 为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为"杨辉三角"
则 展开式中所有项的系数和是

| A. |
128 |
B. |
256 |
C. |
512 |
D. |
1024 |
已知二次函数 的 与 的部分对应值如表:
|
|
0 |
2 |
3 |
4 |
|
5 |
0 |
|
|
0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线 ;③当 时, ;④抛物线与 轴的两个交点间的距离是4;⑤若 , , , 是抛物线上两点,则 ,其中正确的个数是
| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
如图, 是 的直径,直线 与 相切于点 ,过 , 分别作 , ,垂足为点 , ,连接 , ,若 , ,则 的长为
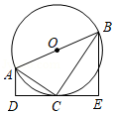
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在直角坐标系中,每个小正方形的边长均为1个单位长度,的顶点坐标分别为,,,△的顶点坐标分别为,,,与△是以点为位似中心的位似图形,则点的坐标为 .

如图,分别以边长为2的等边三角形的三个顶点为圆心,以边长为半径作弧,三段弧所围成的图形是一个曲边三角形,已知是的内切圆,则阴影部分面积为 .

十八大以来,某校已举办五届校园艺术节,为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.

(1)五届艺术节共有 个班级表演这些节目,班数的中位数为 ,在扇形统计图中,第四届班级数的扇形圆心角的度数为 ;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演 “经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用,,,表示),利用树状图或表格求出该班选择和两项的概率.
亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.
(1)计划调配36座新能源客车多少辆?该大学共有多少名志愿者?
(2)若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
如图,在矩形中,,,点在上,将沿折叠,点恰好落在对角线上的点,为上一点,经过点,
(1)求证:是的切线;
(2)在边上截取,点是线段的黄金分割点吗?请说明理由.

如图所示,一种适用于笔记本电脑的铝合金支架,边,可绕点开合,在边上有一固定点,支柱可绕点转动,边上有六个卡孔,其中离点最近的卡孔为,离点最远的卡孔为.当支柱端点放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康,现测得的长为,为,支柱为.
(1)当支柱的端点放在卡孔处时,求的度数;
(2)当支柱的端点放在卡孔处时,,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
参考数据表
计算器按键顺序 |
计算结果(已取近似值) |
|
2.65 |
|
6.8 |
|
11.24 |
|
0.35 |
|
0.937 |
|
41 |
|
49 |
|
49 |
|
41 |

[问题探究]
(1)如图1,和均为等腰直角三角形,,点,,在同一直线上,连接,.
①请探究与之间的位置关系: ;
②若,,则线段的长为 ;
[拓展延伸]
(2)如图2,和均为直角三角形,,,,,.将绕点在平面内顺时针旋转,设旋转角为,作直线,连接,当点,,在同一直线上时,画出图形,并求线段的长.



















 粤公网安备 44130202000953号
粤公网安备 44130202000953号