江苏省扬州市江都区邵樊片七年级上学期期中考试数学试卷
在下面各数中无理数的个数有( )
 ,—3.14,
,—3.14, ,0.1010010001…,+1.99,-
,0.1010010001…,+1.99,-
| A.5个 | B.4个 | C.3个 | D.2个 |
下列各式①m;②x+2=7;③2x+3y;④a>3;⑤ 中,整式的个数有( )
中,整式的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
下面是一个被墨水污染过的方程: ★,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )
★,答案显示此方程的解是x=-1,被墨水遮盖的是一个常数,则这个常数是( )
| A.1 | B.-1 | C. |
D. |
如果A和B都是5次多项式,则下面说法正确的是( )
| A.A-B一定是多项式 |
| B.A-B是次数不低于5的整式 |
| C.A+B一定是单项式 |
| D.A+B是次数不高于5的整式 |
大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和,如23=3+5,33=7+9+11,43=13+15+17+19,…若m3分裂后,其中有一个奇数是103,则m的值是( )
| A.9 | B.10 | C.11 | D.12 |
甲、乙、丙三家超市为了促销一种定价相同的商品,甲超市先降价20%,后又降价10%;乙超市连续两次降价15%;丙超市一次降价30%。那么顾客到__________家超市购买这种商品更合算.
学校文学社组织学生去采风.若租用45座的客车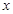 辆,则有20人无法成行;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是 (用含有x的代数式表示)
辆,则有20人无法成行;若租用60座的客车则可少租用2辆,且最后一辆还没坐满,则乘坐最后一辆60座客车的人数是 (用含有x的代数式表示)
圆上有五个点,这五个点将圆分成五等份(每一份称为一段弧长),把这五个点按顺时针方向依次编号为1,2,3,4,5,若从某一点开始,沿圆周顺时针方向行走,点的编号是数字几,就走几段弧长,则称这种走法为一次“移位”.如:小明在编号为3的点,那么他应走3段弧长,即从3→ 4→5→1为第一次“移位”,这时他到达编号为1的点,然后从1→2为第二次“移位”.若小明从编号为4的点开始,第2014次“移位”后,他到达编号为 的点.

有这样一道题:求 ,其中
,其中 .有位同学把
.有位同学把 错抄成
错抄成 ,但他的计算结果也是正确的,试通过计算说明其中的道理.-
,但他的计算结果也是正确的,试通过计算说明其中的道理.-
已知多项式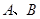 ,计算
,计算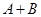 .某同学做此题时误将
.某同学做此题时误将 看成了
看成了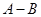 ,求得
,求得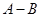 =
=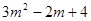 ,若
,若 ,请你帮助他求得正确答案.
,请你帮助他求得正确答案.
(本题10分)定义一种新运算:观察下列式子:




(1)请你想一想:  ;
;
(2)若 ,那么
,那么
 (填入 “=”或 “≠ ”)
(填入 “=”或 “≠ ”)
(3)若 ,请求出
,请求出 的值。
的值。
平安加气站某日7:00前的储气量为10000立方米.加气站在加气过程中每把加气枪均以每小时200立方米的速度为汽车加气.设加气站从7:00开始加气总时间为x(小时)(加气期间关闭加气枪的时间忽略不计).另外,加气站在不同时间段加气枪的使用数量如下:
| 时间段 |
7:00—7:30 |
7:30—8:00 |
8:00以后 |
| 加气枪使用数量 (单位:把) |
2 |
4 |
6 |
(1)7:30时加气站的储气量为 立方米;
(2)当x>1时,试用含x的代数式表示加气站加气x小时后的储气量(答案要求化简);
(3)若每辆车的加气量均为20立方米,试说明前70辆车能否在当天8:30之前加完气?若能,请加以说明;若不能,则8:00以后至少还需添加几把枪加气才能保证在当天8:30之前加完气?
(本题12分)已知数轴上有A、B、C三个点,它们表示的数是﹣24,﹣10,10.
(1)填空:AB=_________,BC= ;
(2)若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和7个单位长度的速度向右运动.设运动时间为t秒,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,用含t的代数式表示BC和AB的长,并探索:BC-AB的值是否随着时间t的变化而改变?请说明理由






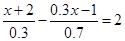 的分母化为整数,结果应为( )
的分母化为整数,结果应为( )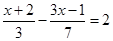
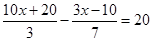
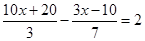
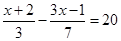
 的次数是 次
的次数是 次  与
与 是同类项,则
是同类项,则 的值是 .
的值是 . ,则代数式
,则代数式 的值为 .
的值为 .
 、
、 在数轴上的位置如图所示,则化简
在数轴上的位置如图所示,则化简 的结果为 .
的结果为 .
 -(-12)÷(-4)
-(-12)÷(-4)



 的方程:
的方程: 与
与 有相同的解,求关于
有相同的解,求关于 的方程
的方程 的解.
的解. +ac值;
+ac值; |,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值.
|,试求4(2a一S)+2(2a﹣S)﹣(2a﹣S)的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号