中考真题分项汇编 第1期 专题3 方程(组)与不等式(组)问题
我省2013年的快递业务量为1.4亿件,受益于电子商务发展和法治环境改善等多重因素,快递业务迅猛发展,2014年增速位居全国第一.若2015年的快递业务量达到4.5亿件,设2014年与2013年这两年的平均增长率为x,则下列方程正确的是( )
| A.1.4(1+x)=4.5 |
| B.1.4(1+2x)=4.5 |
| C.1.4(1+x)2=4.5 |
| D.1.4(1+x)+1.4(1+x)2=4.5 |
利用加减消元法解方程组 ,下列做法正确的是( )
,下列做法正确的是( )
| A.要消去y,可以将①×5+②×2 |
| B.要消去x,可以将①×3+②×(-5) |
| C.要消去y,可以将①×5+②×3 |
| D.要消去x,可以将①×(-5)+②×2 |
若关于x的方程x2+2x+a=0不存在实数根,则a的取值范围是( )
| A.a<l | B.a>1 | C.a≤1 | D.a≥1 |
关于 的一元二次方程
的一元二次方程 有实数根,则
有实数根,则 的取值范围是 ( )
的取值范围是 ( )
A. ≥ ≥ |
B. ≤ ≤ |
C. ≥ ≥ |
D. ≤ ≤ |
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为 米,则可以列出关于
米,则可以列出关于 的方程是( )
的方程是( )

A. |
B. |
C. |
D. |
(.重庆市A卷,第8题,4分)一元二次方程 的根是( )
的根是( )
A. |
B. |
C. |
D. |
(.重庆市B卷,第8题,4分)已知一元二次方程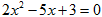 ,则该方程根的情况是( )
,则该方程根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.两个根都是自然数 | D.无实数根 |
分式方程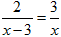 的解为( )
的解为( )
| A.x = 0 | B.x = 3 | C.x =5 | D.x = 9 |
(.重庆市A卷,第17题,4分)从 这五个数中随机抽取一个数记为
这五个数中随机抽取一个数记为 ,
, 的值既是不等式组
的值既是不等式组 的解,又在函数
的解,又在函数 的自变量取值范围内的概率是 .
的自变量取值范围内的概率是 .
(.重庆市B卷,第8题,4分)从-2,-1,0,1,2这5个树种,随机抽取一个数记为a,则使关于x的不等式组 有解,且使关于x的一元一次方程
有解,且使关于x的一元一次方程 的解为负数的概率为________.
的解为负数的概率为________.
《九章算数》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,它的代数成就主要包括开方数、正负数和方程数,其中,方程数是《九章算数》最高的数学成就.
《九章算数》中记载:“今年牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?”
译文:“假设有5头牛,2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”
设每头牛值金x两,每只羊值金y两,可列方程组为____.
关于x的一元二次方程 有两个相等的实数根,写出一组满足条件的实数a,b的值a=____,b=____.
有两个相等的实数根,写出一组满足条件的实数a,b的值a=____,b=____.
(.河南省,第19题,9分)已知关于x的一元二次方程(x-3)(x-2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
(本小题8分)
解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得__________________;
(Ⅱ)解不等式②,得__________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为__________________.
为解决“最后一公里”的交通接驳问题,北京市投放了大量公租自行车供市民使用.到2013年底,全市已有公租自行车25000辆,租赁点600个.预计到2015年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2013年成平均每个租赁点的公租自行车数量的1.2倍.预计2015年底,全市将租赁点多少个?
 的解集在数轴上表示为( ).
的解集在数轴上表示为( ).
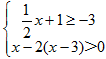 的最大整数解为( )
的最大整数解为( ) 的解是_______________.
的解是_______________. 的一元二次方程
的一元二次方程 没有实数根,那么
没有实数根,那么 的取值范围是________.
的取值范围是________. ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
 >1-
>1- .
.

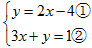
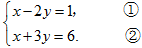
 并写出它的所有非负整数解.
并写出它的所有非负整数解.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号