江苏省无锡市崇安区八年级上学期期中考试数学试卷

下面有4个汽车标志图案，其中是轴对称图形的有（   ）

到一个三角形三个顶点的距离都相等的点是这个三角形的（   ）

青青同学把一张长方形纸折了两次，如图，使点A、B都落在DG上，折痕分别是DE、DF，则∠EDF的度数为（   ）

A．60°        B．75°         C．90°            D．120°

等腰三角形中有一个角等于70º，则它的底角度数是（   ）

如图，∠CAB＝∠DBA，再添一个条件，不一定能判定△ABC≌△BAD的是（   ）

在Rt△ABC中，∠C＝90º，a、b、c分别为∠A、∠B、∠C的对边，已知a：b＝3：4，c＝10，则△ABC的面积为（   ）
A．24            B．12          C．28            D．30

△ABC中，∠A，∠B，∠C的对边分别为a、b、c，下列说法中错误的是（   ）

A．如果∠C－∠B＝∠A，则△ABC是直角三角形，且∠C＝90º；

B．如果，则△ABC是直角三角形，且∠C＝90º；

C．如果（c＋a）（ c－a）＝，则△ABC是直角三角形，且∠C＝90º；

D．如果∠A：∠B：∠C＝3：2：5，则△ABC是直角三角形，且∠C＝90º．

如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE＝5，BC＝8，则△DEF的周长是（   ）

如图，已知Rt△ABC中，∠C＝90º，∠A＝30º，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有（   ）

如图，在△ABC中AD是∠A的外角平分线，P是AD上一动点且不与点A、D重合，记PB＋PC＝a，AB＋AC＝b，则a、b的大小关系是（   ）

A．a＞b         B．a＝b         C．a＜b         D．不能确定

已知△ABC≌△DEF，△ABC的周长为100cm，DE＝30cm，DF＝25cm，那么BC＝      ．

等腰三角形有一边长3cm，周长为13cm，则该等腰三角形的底边为      cm．

如图，AB∥CF，E为DF的中点，若AB＝9cm，CF＝5cm，则BD＝      cm．

如图，在△ABC中，AB＝AC，∠A＝40º，点D在AC上，BD＝BC，则∠ABD的度数为      ．

如图，在△ABC中，∠C＝90º，AB的垂直平分线交BC于点D，∠CAD：∠DAB＝1：2，则∠B的度数为      ．

如图，在Rt△ABC中，∠C＝90º，AD平分∠CAB，AC＝6，BC＝8，CD＝      ．

如图，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD、CE交于点H，已知EH＝EB＝3，AE＝4，则CH的长是      ．

如图，在△ABC中，CD⊥AB于点D，E是AC的中点，若AD＝6，DE＝5，则CD的长为      ．

如图，∠AOB＝30°，点M、N分别在边OA、OB上，且OM＝1，ON＝3，点P、Q 分别在边OB、OA上，则MP＋PQ＋QN的最小值是      ．

如图，在△ABC中，AB＝BC＝4，AO＝BO，P是射线CO上的一个动点，∠AOC＝60°，则当△PAB为直角三角形时，AP的长为      ．

尺规作图（不写作法，保留作图痕迹）
在△ABC的形内求作一点P，使得点P到A、B两点的距离相等，到AB、AC两边的距离也相等．

如图，在△ABC中，AB＝AC，M是BC的中点，D．E分别是AB、AC边上的点，且BD＝CE，求证：MD＝ME．

在△ABC中，AB＝AC＝20，BC＝32，点D在BC上，求出当AD＝13时BD的长．

已知△ABC中，∠C是其最小的内角，如果过顶点B的一条直线把这个三角形分割成了两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为△ABC的关于点B的伴侣分割线．例如：如图1，在Rt△ABC中，∠A＝90°，∠C＝20°，过顶点B的一条直线BD交AC于点D，且∠DBC＝20°，显然直线BD是△ABC的关于点B的伴侣分割线．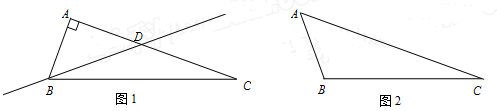

（1）如图2，在△ABC中，∠C＝20°，∠ABC＝110°．请在图中画出△ABC的关于点B 的伴侣分割线，并标注角度；
（2）在△ABC中，设∠B的度数为y，最小内角∠C的度数为x．试探索y与x之间满足怎样的关系时，△ABC存在关于点B的伴侣分割线．

问题探究
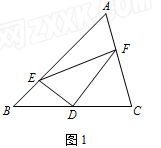
（1）如图1，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
①求证：BE＋CF＞EF；
②若∠A＝90°，探索线段BE、CF、EF之间的等量关系，并加以证明．
问题解决
（2）如图2，在四边形ABDC中，∠B＋∠C＝180°，DB＝DC，∠BDC＝120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．
   

如图1，△ABC中，CD⊥AB于D，且BD ：AD ：CD＝2 ：3 ：4．
（1）试说明△ABC是等腰三角形；
（2）已知S_△ABC＝40cm²，如图2，动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动，同时动点N从点A出发以相同速度沿线段AC向点C运动，当其中一点到达终点时整个运动都停止．设点M运动的时间为t（秒）．
①若△DMN的边与BC平行，求t的值；
②若点E是边AC的中点，问在点M运动的过程中，△MDE能否成为等腰三角形？若能，求出t的值；若不能，请说明理由．