山东省潍坊市中考一模数学试卷
在某次体育测试中,九年级某班7位同学的立定跳远成绩(单位:m)分别为:2.15、2.25、2.25、2.31、2.42、2.50、2.51,则这组数据的中位数是( )
| A.2.15 | B.2.25 | C.2.31 | D.2.42 |
如图是一个由6个大小相同、棱长为1的小正方体搭成的几何体,关于它的下列说法中正确的是( )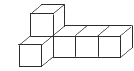
| A.主视图的面积为6 | B.左视图的面积为2 |
| C.俯视图的面积为5 | D.三种视图的面积都是5 |
2014年,潍坊市扎实推进农村中小学校舍标准化建设,完成投资约11.64亿元,全面改善了农村学校的办学条件,推动了全市义务教育的均衡发展.数字“11.64亿”用科学记数法可表示为( )
| A.11.64 | B.11.64×108 | C. 1.164×109 | D.116.4×107 |
如图,直线l是一条河,A、B两地相距5km,A、B两地到l的距离分别为3km、6km,欲在l上的某点M处修建一个水泵站,向A、B两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( ) 
已知实数x、y同时满足三个条件:①x-y=2-m,②4x-3y=2+m,③x>y,那么实数m的取值范围是( )
| A.m>-2 | B.m<2 | C.m<-2 | D.m>2 |
如图,AB是⊙O的直径,D、C在⊙O上,AD∥OC,∠DAB=60°,连接AC,则∠DAC等于( )
A、15° B、30° C、45° D、60°
关于x的方程mx2−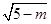 x-1=0有两个实数解,则m的取值范围是( )
x-1=0有两个实数解,则m的取值范围是( )
A.m≥-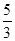 |
| B.0<m≤5 |
C.-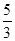 ≤m≤5且m≠0 ≤m≤5且m≠0 |
| D.0<m≤5且m≠0 |
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(0,4)、(-3,0),点E、F分别为AB、BO的中点,分别连接AF、EO,交点为P,点P坐标为( )
A、(- ,
, ) B、(-
) B、(- ,2) C、(-1,
,2) C、(-1, ) D、(-1,2)
) D、(-1,2)
如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2,则它移动的距离AA′等于( )
| A.0.5cm | B.1cm | C.1.5cm | D.2cm |
如图,等腰梯形OABC的顶点B、C在第一象限,点A的坐标为(5,0),点D为边AB的中点,反比例函数y= (x>0)的图象经过C,D两点,若∠COA=60°,则k的值和梯形的面积分别是( )
(x>0)的图象经过C,D两点,若∠COA=60°,则k的值和梯形的面积分别是( )
A、 ,4
,4 B、2
B、2 ,4
,4 C、4
C、4 ,12
,12 D、4
D、4 ,6
,6
有三张背面完全相同的卡片上分别写有一个整式,把它们背面朝上洗匀,小明从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张,第一次抽取的卡片上的整式做分子,第二次抽取的卡片上的整式做分母,则能组成分式的概率是 .
二次函数y=x2-6x+n的部分图象如图所示,若关于x的一元二次方程x2-6x+n=0的一个解为x1=1,则另一个解x2= .
在平面直角坐标系A中,已知直线l:y=x,作A1(1,0)关于y=x的对称点B1,将点B1向右水平平移2个单位得到点A2;再作A2关于y=x的对称点B2,将点B2向右水平平移2个单位得到点A3;….按此规律,.则点B2014的坐标是
为响应推进中小学生素质教育的号召,某校决定在下午15点至16点开设以下选修课:音乐史、管乐、篮球、健美操、油画.为了解同学们的选课情况,某班数学兴趣小组从全校三个年级中各调查一个班级,根据相关数据,绘制如下统计图.
(1)请根据以上信息,直接补全条形统计图(图1)和扇形统计图(图2);
(2)若初一年级有180人,请估算初一年级中有多少学生选修音乐史?
(3)若该校共有学生540人,请估算全校有多少学生选修篮球课?
某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:
(1)求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动,
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
如图,⊙O是△ABC的外接圆,AB=AC,连结CO并延长交⊙O的切线AP于点P.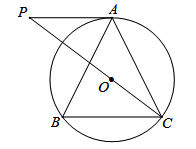
(1)求证:∠APC=∠BCP;
(2)若sin∠APC=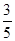 ,BC=4,求AP的长.
,BC=4,求AP的长.
如图,两条公路AB,CD(均视为直线).东西向公路CD段限速,规定最高行驶速度不能越过60千米/时,并在南北向公路离该公路100米的A处没置了一个监测点.已知点C在A的北偏西60°方向上,点D在A的北偏东45°方向上.
(1)经监测,一辆汽车从点C匀速行驶到点D所的时间是15秒,请通过计算,判断该汽车在这段限速路上是否超速?(参考数据: =1.732)
=1.732)
(2)若一辆大货车在限速路上由D处向西行驶,一辆小汽车在南北向公路上由A处向北行驶,设两车同时开出且小汽车的速度是大货车速度的2倍,两车在匀速行驶过程中的最近距离是多少?
如图1,是边长分别为6和4的两个等边三角形纸片ABC和CD1E1叠放在一起.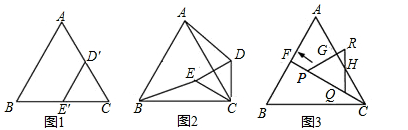
(1)操作:固定△ABC,将△CD1E1绕点C顺时针旋转得到△CDE,连接AD、BE,如图2.探究:在图2中,线段BE与AD之间有怎样的大小关系?并请说明理由;
(2)操作:固定△ABC,若将△CD1E1绕点C顺时针旋转30°得到△CDE,连接AD、BE,CE的延长线交AB于点F,在线段CF上沿着CF方向平移,(点F与点P重合即停止平移)平移后的△CDE设为△PQR,如图3.
探究:在图3中,除三角形ABC和CDE外,还有哪个三角形是等腰三角形?写出你的结论(不必说明理由);
(3)探究:如图3,在(2)的条件下,设CQ=x,用x代数式表示出GH的长.

 和-3
和-3
 的图象如图,则二次函数y=2kx2-x+k2的图象大致为( )
的图象如图,则二次函数y=2kx2-x+k2的图象大致为( )
 有增根,则m的值为 .
有增根,则m的值为 . , BC⊥OA于点C,则图中阴影部分的面积为 .(结果保留π)
, BC⊥OA于点C,则图中阴影部分的面积为 .(结果保留π)
 粤公网安备 44130202000953号
粤公网安备 44130202000953号