2015年初中毕业升学考试(贵州六盘水卷)数学
如图,直线l1和直线l2被直线l所截,已知l1∥l2,∠1=70°,则∠2=( )
| A.110° | B.90° | C.70° | D.50° |
袋中有5个红球、4个白球、3个黄球,每一个球除颜色外都相同,从袋中任意摸出一个球是白球的概率( )
A. |
B. |
C. |
D. |
如图是正方体的一个平面展开图,原正方体上两个“我”字所在面的位置关系是( )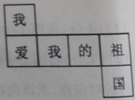
| A.相对 | B.相邻 | C.相隔 | D.重合 |
下列说法不正确的是( )
| A.圆锥的俯视图是圆 |
| B.对角线互相垂直平分的四边形是菱形 |
| C.任意一个等腰三角形是钝角三角形 |
| D.周长相等的正方形、长方形、圆,这三个几何图形中,圆面积最大 |
“魅力凉都六盘水”某周连续7天的最高气温(单位°C)是26,24,23,18,22,22,25,则这组数据的中位数是( )
A.18 B.22 C.23 D.24
如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
| A.∠A=∠D | B.AB=DC | C.∠ACB=∠DBC | D.AC=BD |
如图,假设篱笆(虚线部分)的长度16m,则所围成矩形ABCD的最大面积是( )
| A.60m2 | B.63m2 | C.64m2 | D.66m2 |
观察中国象棋的棋盘,其中红方“马”的位置可以用一个数对(3,5)来表示,红“马”走完“马3进
四”后到达B点,则表示B点位置的数对是: .
如图8,有一个英语单词,四个字母都关于直线l对称,请在试卷上补全字母,在答题卡上写出这个单
词所指的物品 .
2014年10月24日,“亚洲基础设施投资银行”在北京成立,我国出资500亿美元,这个数用科学记数法表示为 美元
在正方形A1B1C1O和A2B2C2C1,按如图9所示方式放置,在直线 上,点C1,C2在x轴上,已知A1点的坐标是(0,1),则点B2的坐标为 .
上,点C1,C2在x轴上,已知A1点的坐标是(0,1),则点B2的坐标为 .
赵洲桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙。
如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R= 米.
(本小题8分)如图,已知, l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上,设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.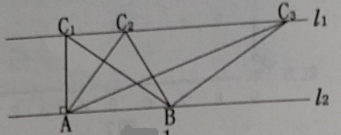
(本小题10分)联通公司手机话费收费有A套餐(月租费15元,通话费每分钟0.1元)和B套餐(月租费0元,通话费每分钟0.15元)两种。设A套餐每月话费为y1(元),B套餐每月话费为y2(元),月通话时间为x分钟.
(1)分别表示出y1与x,y2与x的函数关系式.
(2)月通话时间为多长时,A、B两种套餐收费一样?
(3)什么情况下A套餐更省钱?
(本小题10分)毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究: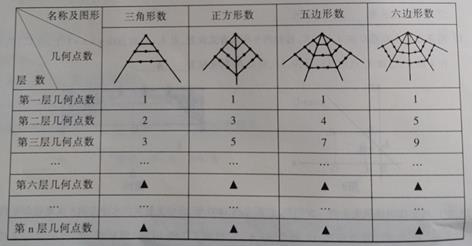
请在答题卡上写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
(本小题12分)某学校对某班学生“五·一”小长假期间的度假情况进行调查,并根据收集的数据绘制了两幅不完整的统计图,请你根据图中提供的信息解答下面的问题:
(1)求出该班学生的总人数.
(2)补全频数分布直方图.
(3)求出扇形统计图中∠α的度数.
(4)你更喜欢哪一种度假方式.
(本小题12分)如图12,在Rt△ACB中,∠ACB=90°,点O是AC边上的一点,以O为圆心,OC为半径的圆与AB相切于点D,连接OD.
(1)△ADO∽△ACB.
(2)若⊙O的半径为1,求证:AC=AD·BC
(本小题12分)如图,已知Rt△ACB中,∠C=90°,∠BAC=45°.
(1)用尺规作图,:在CA的延长线上截取AD=AB,并连接BD(不写作法,保留作图痕迹)
(2)求∠BDC的度数.
(3)定义:在直角三角形中,一个锐角A的邻边与对边的比叫做∠A的余切,记作cotA,即 ,根据定义,利用图形求cot22.5°的值.
,根据定义,利用图形求cot22.5°的值.
(本小题16分)如图,已知图①中抛物线 经过点D(-1,0),D(0,-1),E(1,0).
经过点D(-1,0),D(0,-1),E(1,0).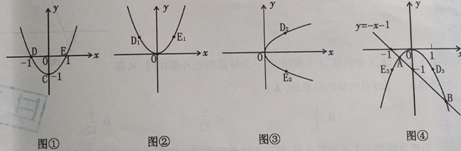
(1)求图①中抛物线的函数表达式.
(2)将图①中的抛物线向上平移一个单位,得到图②中的抛物线,点D与点D1是平移前后的对应点,
求该抛物线的函数表达式.
(3)将图②中的抛物线绕原点O顺时针旋转90°后得到图③中的抛物线,所得到抛物线表达式为 ,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.
,点D1与D2是旋转前后的对应点,求图③中抛物线的函数表达式.
(4)将图③中的抛物线绕原点O顺时针旋转90°后与直线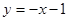 相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.
相交于A、B两点,D2与D3是旋转前后如图④,求线段AB的长.

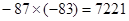

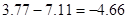
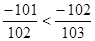
 的点在数轴上表示时,所在哪两个字母之间( )
的点在数轴上表示时,所在哪两个字母之间( )

 的一个根,则方程的另一个根x2是 .
的一个根,则方程的另一个根x2是 . .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号