江苏苏州市高新区七年级下学期期中测试数学试卷
1.甲型H7N9流感病毒的直径大约为0.000 000 08米,用科学记数法表示为( )
| A.0.8×10-7米 | B.8×10-8米 | C.8×10-9米 | D.8×10-7米 |
若某三角形的两边长分别为3和4,则下列长度的线段能作为其第三边的是( )
| A.1 | B.5 | C.7 | D.9 |
如图,能判定EB∥AC的条件是( )
| A.∠C=∠ABE | B.∠A=∠EBD |
| C.∠C=∠ABC | D.∠A=∠ABE |
下列计算正确的是( )
| A.(a3)2=a6 | B.a8÷a2=a4 |
| C.a3·a2=a6 | D.(-ab)2=2a2b2 |
如图,∠1+∠2的度数是 ( )

|
A.90° B.135° C.180° D.270°
若a=(-99)0,b=(-0.1)-1, ,那么a,b,c的大小关系为 ( )
,那么a,b,c的大小关系为 ( )
| A.a>b>c | B.c>a>b | C.a>c>b | D.c>b>a |
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=60°,∠ABC=80°,则∠CBE的度数为( )
| A.30° | B.40° | C.60° | D.80° |
计算(﹣2)100+(﹣2)99所得的结果是( )
| A.﹣299 | B.﹣2 | C.299 | D.2 |
下列说法不正确的是 ( )
| A.三角形三个内角的和等于180° |
| B.两直线平行,同位角相等 |
| C.过一点有且只有一条直线平行于已知直线 |
| D.对顶角相等 |
计算机是将信息转换成二进制数进行处理的,二进制即“逢2进1”,如(1101)2表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数(1111)2转换成十进制形式是数( )
| A.8 | B.15 | C.20 | D.30 |
定义:如果一个数的平方等于–1,记为i2=–1,这个数i叫做虚数单位.那么
 ,
, ,
, ,那么
,那么 .
.
如图,A,B,C分别是线段A1B,B1C,C1A的中点,若△ABC的面积是1,
那么△A1B1C1的面积_______.
如图,在△ABC中,.∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得∠A2;……;∠A2013BC与∠A2013CD的平分线相交于点A2014,得∠A2014 .如果∠A=n度,则∠A2014= 度.(直接用含n的代数式表示)
(本题满分20分,每小题5分)计算:
(1)a2•a4+(﹣a2)3
(2)
(3)(-3)0+( )-1+(-2)3×2-4
)-1+(-2)3×2-4
(4)
(本题4分)正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
(1)请画出平移后的△A′B′C′.
(2)△A′B′C′的面积为___________.
(3)若连接AA′,CC′,则这两条线段之间的关系是__ _.
(本题5分)先化简,再求值:a3•(﹣b3)2 +( a b2)3 ,其中a=
a b2)3 ,其中a= ,b=
,b= .
.
(本题6分)如图,在△ABC中,CF⊥AB于F,ED⊥AB于D,∠1=∠2.
(1)求证:FG∥BC
(2)若∠A=60°,∠AFG=40°,求∠ACB的度数.
(本题6分)我们知道一般地,加减运算是互逆运算,乘除运算也是互逆运算;其实乘方运算也有逆运算;如我们规定式子23=8可以变形为log28=3,log525=2也可以变形为52=25.在式子23=8中,3叫做以2为底8的对数,记为log2 8.一般地,若an=b(a>0且a≠1,b>0),则n叫做以a为底b的对数,记为logab(即logab=n).
根据上面的规定,请解决下列问题:
(1)计算:log3 1= ,log10100= ;
(2)已知x=log32,y=log318,请你用x的代数式来表示y.(请写出必要的过程)
(本题9分)小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,判断BD、MF的位置关系是 ;请证明你的结论。
(2)如图②,M为边AC反向延长线上一点,直接判断BD、MF的位置关系是 。
(3)如图③,M为边AC延长线上一点,判断BD、MF的位置关系是 ;请证明你的结论.
如图1,在Rt△ABC中,∠ACB=90°,D是AB上一点,且∠ACD=∠B,
(1)判断CD与AB的位置关系为 ;
(2)如图2,若E为BC上一点,AE交CD于点F,BC=3CE,AB=4AD,△ABC、△CEF、△ADF的面积分别为S△ABC、S△CEF、S△ADF,且S△ABC=36,则S△CEF-S△ADF= . 

 ,则
,则 .
.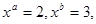 则xa-b = .
则xa-b = .

 ,求m的值。
,求m的值。 的值,我们可以采用如下的方法:
的值,我们可以采用如下的方法: ①,则
①,则 ②,
②, ,所以
,所以 .
. 的值为 .
的值为 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号