天津市南开区高三一模文科数学试卷
设A,B为两个不相等的集合,条件 , 条件
, 条件 ,则p是q的( ).
,则p是q的( ).
| A.充分不必要条件 | B.充要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
如图,是一个几何体的三视图,其中主视图、左视图是直角边长为2的等腰直角三角形,俯视图为边长为2的正方形,则此几何体的表面积为( ).
A.8+4 |
B.8+4 |
C. |
D.8+2 +2 +2 |
已知双曲线 的一条渐近线方程是
的一条渐近线方程是 ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,则双曲线的方程为( ).
的准线上,则双曲线的方程为( ).
| A.4x2–12y2=1 | B.4x2– y2=1 y2=1 |
| C.12x2–4y2=1 | D.  |
已知函数 (
( >0)的图象与x轴的两个相邻交点的距离等于
>0)的图象与x轴的两个相邻交点的距离等于 ,若将函数y=f(x)的图象向左平移
,若将函数y=f(x)的图象向左平移 个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( ).
个单位得到函数y=g(x)的图象,则y=g(x)是减函数的区间为( ).
A.(– ,0) ,0) |
B.(– , , ) ) |
C.(0, ) ) |
D.( , , ) ) |
已知函数 f(x)=|mx|–|x–1|(m>0),若关于x的不等式
f(x)=|mx|–|x–1|(m>0),若关于x的不等式 的解集中的整数恰有3个,则实数m的取值范围为( ).
的解集中的整数恰有3个,则实数m的取值范围为( ).
| A.0<m≤1 | B.   |
C.1<m< |
D. ≤m<2 ≤m<2 |
如图是某学校抽取的学生体重的频率分布直方图,已知图中从左到右的前3个小组的频率依次成等差数列,第2小组的频数为15,则抽取的学生人数为 .
如图,圆O的割线PAB交圆O于A、B两点,割线PCD经过圆心O.已知PA=AB= ,PO=8.则BD的长为 .
,PO=8.则BD的长为 .
已知正三角形ABC的边长为2,点D,E分别在边AB,AC上,且 =
= 
 ,
, =
= 
 .若点F为线段BE的中点,点O为△ADE的重心,则
.若点F为线段BE的中点,点O为△ADE的重心,则 •
• = .
= .
(本小题满分13分)某高中从学生体能测试结果中随机抽取100名学生的测试结果,按体重(单位:kg)分组,得到的频率分布表如右图所示.
| 组号 |
分组 |
频数 |
频率 |
| 第1组 |
[50,55) |
5 |
0.050 |
| 第2组 |
[55,60) |
① |
0.350 |
| 第3组 |
[60,65) |
30 |
② |
| 第4组 |
[65,70) |
20 |
0.200 |
| 第5组 |
[70,75] |
10 |
0.100 |
| 合计 |
100 |
1.000 |
(Ⅰ)请求出频率分布表中①、②位置相应的数据;
(Ⅱ)从第3、4、5组中用分层抽样抽取6名学生进行第二次测试,求第3、4、5组每组各抽取多少名学生进入第二次测试?
(Ⅲ)在(Ⅱ)的前提下,在6名学生中随机抽取2名学生由李老师进行测试,求第4组至少有一名学生被李老师测试的概率?
(本小题满分13分)在非等腰△ABC中,a,b,c分别是三个内角A,B,C的对边,且a=3,c=4,C=2A.
(Ⅰ)求cosA及b的值;
(Ⅱ)求cos( –2A)的值.
–2A)的值.
(本小题满分14分)如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,PC=AB=2AD=2CD=2,E是PB的中点.
(Ⅰ)求证:平面EAC⊥平面PBC;
(Ⅱ)求二面角P-AC-E的余弦值;
(Ⅲ)求直线PA与平面EAC所成角的正弦值.
(本小题满分13分)设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和,已知b1≠0,2bn–b1=S1•Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bn•log3an,求数列{cn}的前n项和Tn.
(本小题满分14分)已知椭圆C: (a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为
(a>b>0)与y轴的交点为A,B(点A位于点B的上方),F为左焦点,原点O到直线FA的距离为 b.
b.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设b=2,直线y=kx+4与椭圆C交于不同的两点M,N,求证:直线BM与直线AN的交点G在定直线上.
 =( ).
=( ).

 –
– i
i +
+ i
i ,则目标函数
,则目标函数 的最小值是( ).
的最小值是( ). 的值域是( ).
的值域是( ). 依次成等比数列,则
依次成等比数列,则 = .
= .
 作圆
作圆 的两条切线,切点分别为A,B,则直线AB的方程为 .
的两条切线,切点分别为A,B,则直线AB的方程为 .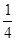 –
–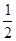 ln2.
ln2. 粤公网安备 44130202000953号
粤公网安备 44130202000953号