北京市东城区示范校高三上学期综合能力测试理科数学试卷
设 为非零常数,则“
为非零常数,则“ 与
与 解集相同”是“
解集相同”是“ ”的
”的
| A.既不充分也不必要条件 |
| B.充分必要条件 |
| C.必要而不充分条件 |
| D.充分而不必要条件 |
已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸(单位: ),可得这个几何体的体积是__________
),可得这个几何体的体积是__________ .
.
如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,则DM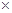 DN=____________.
DN=____________.
某市电信宽带私人用户月收费标准如下表:假定每月初可以和电信部门约定上网方案.
| 方案 |
类别 |
基本费用 |
超时费用 |
| 甲 |
包月制 |
70元 |
|
| 乙 |
有限包月制(限60小时) |
50元 |
0.05元/分钟(无上限) |
| 丙 |
有限包月制(限30小时) |
30元 |
0.05元/分钟(无上限) |
若某用户每月上网时间为66小时,应选择__________方案最合算.
圆O的半径为1,P为圆周上一点,现将如图装置的边长为1的正方形(实线所示,正方形的顶点A与点P重合)沿圆周顺时针滚动,经过若干次滚动,点A第一次回到点P的位置,则点A走过的路径的长度为____________.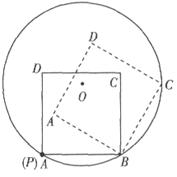
(本小题满分13分)在△ABC中,角A,B,C所对的边分别为 ,满足
,满足 ,且
,且 .
.
(1)求C的大小;
(2)求 的最大值,并求取得最大值时角A,B的值.
的最大值,并求取得最大值时角A,B的值.
(本小题满分13分)如图,四棱锥 中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
中,PA⊥平面ABCD,∠ABC=∠BAD=90°,AD=2PA=2AB=2BC=2.
(1)求三棱锥 的外接球的体积;
的外接球的体积;
(2)求二面角 与二面角
与二面角 的正弦值之比.
的正弦值之比.
(本小题满分13分)设集合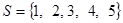 ,从S的所有非空子集中,等可能地取出一个.
,从S的所有非空子集中,等可能地取出一个.
(1)设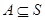 ,若
,若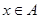 ,则
,则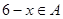 ,就称子集A满足性质
,就称子集A满足性质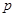 ,求所取出的非空子集满足性质
,求所取出的非空子集满足性质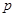 的概率;
的概率;
(2)所取出的非空子集的最大元素为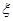 ,求
,求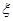 的分布列和数学期望
的分布列和数学期望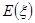 .
.
(本小题满分14分)如图,已知椭圆 的左焦点为F(
的左焦点为F( ,0),过点M(-3,0)作一条斜率大于0的直线
,0),过点M(-3,0)作一条斜率大于0的直线 与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
与椭圆W交于不同的两点A、B,延长BF交椭圆W于点C.
(1)求椭圆W的离心率;
(2)若∠MAC=60°,求直线 的斜率.
的斜率.
(本小题满分13分)已知定义在 上的函数
上的函数 ,
, .
.
(1)求证: 存在唯一的零点,且零点属于(3,4);
存在唯一的零点,且零点属于(3,4);
(2)若 且
且 对任意的
对任意的 恒成立,求
恒成立,求 的最大值.
的最大值.
 ,则下列结论正确的是
,则下列结论正确的是



 的焦距为
的焦距为
 的展开式中常数项为A,则A=
的展开式中常数项为A,则A=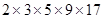 ”之值,则判断框内不能填入
”之值,则判断框内不能填入
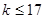 ?
?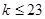
 ?
?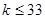 ?
? 有唯一的零点,则实数
有唯一的零点,则实数 的值为
的值为 ,集合
,集合 ,若
,若 ,则实数
,则实数 的取值范围是
的取值范围是



 不等式
不等式 在
在 上恒成立,则实数
上恒成立,则实数 的取值范围是
的取值范围是



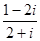 的虚部为__________.
的虚部为__________. 的前
的前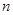 项和记为
项和记为 ,若
,若 ,
,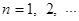 ,则数列
,则数列 _______________.
_______________. ,数列
,数列 :
: 是1,2,…,
是1,2,…, 的一个排列,定义E(
的一个排列,定义E( ,…,
,…, )
) 为数列
为数列 ,
, ,…,
,…, 时,求数列
时,求数列 ,求满足条件的数列
,求满足条件的数列 粤公网安备 44130202000953号
粤公网安备 44130202000953号