福建省四地六校联考高二上学期第一次月考理科数学卷
下列给出的输入语句、输出语句和赋值语句:
(1)输出语句INPUT  ,b,c
,b,c
(2)输入语句INPUT  =3
=3
(3)赋值语句3=A
(4)赋值语句A=B=C
则其中正确的个数是( )
| A.0 | B.1 | C.2 | D.3 |
用秦九韶算法计算多项式 在x=2时,
在x=2时, 的值为( )
的值为( )
| A.2 | B.19 | C.14 | D.33 |
把黑、红、白3张纸牌分给甲、乙、丙三人,则事件“甲分得红牌”与“乙分得红牌”是( )
| A.对立事件 | B.互斥但不对立事件 |
| C.不可能事件 | D.必然事件 |
如图给出的是计算 的值的一个框图,其中菱形判断框内应填入的条件是( )
的值的一个框图,其中菱形判断框内应填入的条件是( )
A. ? ? |
B. ? ? |
C. ? ? |
D. ? ? |
从2 004名学生中抽取50名组成参观团,若采用下面的方法选取,先用简单随机抽样从2 004人中剔除4人,剩下的2 000人再按系统抽样的方法进行,则每人入选的概率是( )
| A.不全相等 |
| B.均不相等 |
C.都相等,且为 |
D.都相等,且为 |
从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:
身高  (cm) (cm) |
160 |
165 |
170 |
175 |
180 |
| 体重y(kg) |
63 |
66 |
70 |
72 |
74 |
根据上表可得回归直线方程 ,据此模型预报身高为172 cm的高三男生的体重为( )
,据此模型预报身高为172 cm的高三男生的体重为( )
A.70.09 B.70.12 C.70.55 D.71.05
如图,大正方形靶盘的边长为 ,四个全等的直角三角形围成一个小正方形,即阴影区域.较短的直角边长为2,现向大正方形靶盘投掷飞镖,则飞镖落在阴影区域的概率为( )
,四个全等的直角三角形围成一个小正方形,即阴影区域.较短的直角边长为2,现向大正方形靶盘投掷飞镖,则飞镖落在阴影区域的概率为( )
A. |
B. |
C. |
D. |
已知 与y之间的几组数据如下表:
与y之间的几组数据如下表:
 |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为 ,则以下结论正确的是( )
,则以下结论正确的是( )
A. B.
B.
C. D.
D.
我校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为__________________
点P( ,3)到直线
,3)到直线 的距离等于4,且在不等式
的距离等于4,且在不等式 表示的平面区域内,则P点的坐标为__________.
表示的平面区域内,则P点的坐标为__________.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后, 统计了他们的成绩,得到如图所示的频率分布直方图.这40个考生成绩的众数 ,中位数 .
已知圆M:(x+cosq)2+(y-sinq)2=1,直线l:y=kx,下面四个命题:
| A.对任意实数k与q,直线l和圆M相切; |
| B.对任意实数k与q,直线l和圆M有公共点; |
| C.对任意实数q,必存在实数k,使得直线l与和圆M相切; |
| D.对任意实数k,必存在实数q,使得直线l与和圆M相切. |
其中真命题的代号是______________(写出所有真命题的代号)
直线 过点P(
过点P( ,2),且与
,2),且与 轴,y轴的正方向分别交于A,B两点,当△AOB的面积为6时,求直线
轴,y轴的正方向分别交于A,B两点,当△AOB的面积为6时,求直线 的方程.
的方程.
(本小题满分13分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,从统计学的角度(在平均数、方差或标准差中选两个)考虑,你认为选派哪位学生参加合适?请说明理由.
(本小题满分13分)一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4,
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率;
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
(本小题满分13分)在长度为10的线段内任取两点将线段分为三段,求这三段可以构成三角形的概率.
(本小题14分)为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:

(Ⅰ)填充频率分布表的空格(将答案直接填在表格内);
| 分组 |
频数 |
频率 |
| 50.5~60.5 |
4 |
0.08 |
| 60.5~70.5 |
|
0.16 |
| 70.5~80.5 |
10 |
|
| 80.5~90.5 |
16 |
0.32 |
| 90.5~100.5 |
|
|
| 合计 |
50 |
1.00 |
(Ⅱ)补全频数直方图;
(Ⅲ)学校决定成绩在75.5~85.5分的学生为二等奖,问该校获得二等奖的学生约为多少人?




 始终平分圆
始终平分圆 的周长,则
的周长,则 的最小值为 ( )
的最小值为 ( )

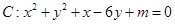 和直线
和直线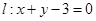
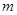 的取值范围;
的取值范围;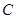 与直线
与直线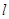 相切时,求圆
相切时,求圆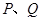 两点,是否存在
两点,是否存在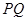 为直径的圆经过原点
为直径的圆经过原点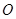 ?
? 粤公网安备 44130202000953号
粤公网安备 44130202000953号