四川省广安市武胜县赛马初中九年级上期末考试模拟考试数学试卷
下列事件中,是必然发生的事件是 ( )
| A.打开电视机,正在播放新闻 |
| B.父亲的年龄比儿子的年龄大 |
| C.通过长期努力学习,你会成为数学家 |
| D.下雨天,每个人都打着雨伞 |
下面图形中是轴对称不是中心对称图形的是 ( )
| A.正方形 | B.正六边形 | C.圆 | D.正五边形 |
甲、乙两个不透明的口袋中分别装有1个红球、2个黄球和2个红球、4个黄球,把它们分别搅匀,分别从甲、乙两个袋中摸出1个球。现给出下列说法:①从甲袋中摸出红球的概率比从乙袋中摸出红球的概率小;②从甲袋中摸出红球的概率与从乙袋中摸出红球的概率相等;③从甲袋中摸出红球的概率是从乙袋中摸出红球的概率的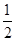 . 其中正确的说法是( )
. 其中正确的说法是( )
| A.①② | B.② | C.②③ | D.①②③ |
在平面直角坐标系xOy中,A点坐标为(3,4),将OA绕原点O顺时针旋转180°得到OA′,则点A′的坐标是( )
A.(-4,3) B.(-3,-4) C.(-4,-3) D.(-3,4)
如果⊙0的半径为10cm,,点P到圆心的距离为8cm,则点P和⊙0的位置关系是( ).
| A.点P在⊙0内 | B.点P在⊙0上 | C.点P在⊙0外 | D.不能确定 |
已知抛物线y=a(x-2)2+k(a>0,a,k为常数),A(-3,y1)B(3,y2)C(4,y3)是抛物线上三点,则y1,y2,y3由小到大依序排列为( )
| A.y1<y2<y3 | B.y2<y1<y3 | C.y2<y3<y1 | D.y3<y2<y1 |
如图,在平面直角坐标系中,抛物线 经过平移得到抛物线
经过平移得到抛物线 ,其对称轴与两段抛物线所围成的阴影部分的面积是( )
,其对称轴与两段抛物线所围成的阴影部分的面积是( )
| A.2 | B.4 | C.8 | D.16 |
从一副扑克牌中取出1张红桃、2张黑桃共3张牌,将这3张牌洗匀后,从中任取1张牌恰好是黑桃的概率是 .
若将抛物线y= x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的解析式是
x2先向左平移2个单位,再向下平移1个单位得到新的抛物线,则新抛物线的解析式是
若一个边长为a的正多边形的内角和等于720°,则这个正多边形的外接圆与内切圆的面积的比是 .
已知二次函数y=2(x﹣3)2+1,下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.则其中说法正确的有
如图所示,△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若∠DEF=52°,则∠A的度数是 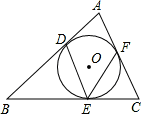
如图所示,已知在 中,
中,  ,
, ,分别以
,分别以 ,
, 为直径作半圆,面积分别记为
为直径作半圆,面积分别记为 ,
, ,则
,则 +
+ 的值等于__________.
的值等于__________.
在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.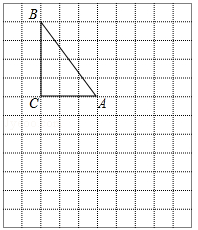
(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2)
(1)求m的值和抛物线的关系式;
(2)求不等式x2+bx+c>x+m的解集(直接写出答案).
关x的一元二次方程(x-2)(x-3)=m有两个实数根x1、x2,
(1)求m的取值范围;
(2)若x1、x2满足等式x1x2-x1-x2+1=0,求m的值.
某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)请用列表或画树形图的方法求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率
如图所示,点 在
在 的直径
的直径 的延长线上,点
的延长线上,点 在
在 上,且
上,且 ,∠
,∠ °.
°.
(1)求证: 是
是 的切线;
的切线;
(2)若 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
杂技团进行杂技表演,演员从跷跷板右端A处弹跳到人梯顶端椅子B处,其身体(看成一个点)的路线是抛物线y=- x2+3x+1的一部分.
x2+3x+1的一部分.
(1)求演员弹跳离地面的最大高度;
(2)已知人梯高BC=3.4米,在一次表演中,人梯到起跳点A的水平距离是4米,问这次表演是否成功?说明理由.
 是关于
是关于 的一元二次方程,则m的值应为( )
的一元二次方程,则m的值应为( ) =2
=2

 的一元二次方程有实数根的是( )
的一元二次方程有实数根的是( )



 ;
; ;
;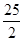 ),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0)
),与x轴交于A、B两点,与y轴交于点C,其中B点坐标为(1,0)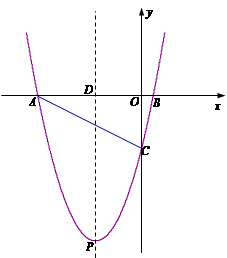
 粤公网安备 44130202000953号
粤公网安备 44130202000953号