北京市海淀区九年级上学期期末考试数学试卷
方程 的根的情况是( )
的根的情况是( )
| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.没有实数根 | D.无法确定是否有实数根 |
小丁去看某场电影,只剩下如图所示的六个空座位供他选择,座位号分别为1号、4号、6号、3号、5号和2号.若小丁从中随机抽取一个,则抽到的座位号是偶数的概率是( )
A. |
B. |
C. |
D. |
如图,△ABC和△A1B1C1是以点O为位似中心的位似三角形,若C1为OC的中点,AB=4,则A1B1的长为 ( )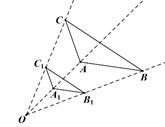
| A.1 | B.2 | C.4 | D.8 |
已知点A( ,
, ),B(
),B( ,
, )是反比例函数
)是反比例函数 的图象上的两点,若
的图象上的两点,若 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.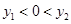 |
B.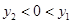 |
C. |
D. |
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作 OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为 ( )
A. |
B. |
C.1 | D.2 |
如图,已知矩形ABCD的长AB为5,宽BC为4,E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )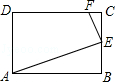
A. |
B. |
C. |
D. |
在某一时刻,测得一根高为2m的竹竿的影长为1m,同时测得一栋建筑物的影长为12m,那么这栋建筑物的高度为 m.
对于正整数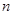 ,定义
,定义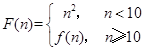 ,其中
,其中 表示
表示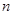 的首位数字、末位数字的平方和.例如:
的首位数字、末位数字的平方和.例如: ,
, .
.
规定 ,
, (
( 为正整数).例如:
为正整数).例如: ,
,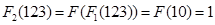 .
.
(1)求: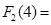 ____________,
____________,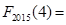 ______________;
______________;
(2)若 ,则正整数m的最小值是_____________.
,则正整数m的最小值是_____________.
如图,在平面直角坐标系 中,正比例函数
中,正比例函数 与反比例函数
与反比例函数 的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
的图象交于A,B两点,A点的横坐标为2,AC⊥x轴于点C,连接BC.
(1)求反比例函数的解析式;
(2)若点P是反比例函数 图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
图象上的一点,且满足△OPC与△ABC的面积相等,请直接写出点P的坐标.
如图,△ABC中,∠ACB=90°,sinA= , BC=8,D是AB中点,过点B作直线CD的垂线,垂足为E.
, BC=8,D是AB中点,过点B作直线CD的垂线,垂足为E.
(1)求线段CD的长;
(2)求 的值.
的值.
某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):
为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
如图,四边形ABCD是平行四边形,点A,B,C在⊙O上,AD与⊙O相切,射线AO交BC于点E,交⊙O于点F.点P在射线AO上,且∠PCB=2∠BAF.
(1)求证:直线PC是⊙O的切线;
(2)若AB= ,AD=2,求线段PC的长.
,AD=2,求线段PC的长.
阅读下面材料:
小明观察一个由 正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
正方形点阵组成的点阵图,图中水平与竖直方向上任意两个相邻点间的距离都是1.他发现一个有趣的问题:对于图中出现的任意两条端点在点阵上且互相不垂直的线段,都可以在点阵中找到一点构造垂直,进而求出它们相交所成锐角的正切值.
请回答:(1)如图1,A、B、C是点阵中的三个点,请在点阵中找到点D,作出线段CD,使得CD⊥AB;
(2)如图2,线段AB与CD交于点O.为了求出 的正切值,小明在点阵中找到了点E,连接AE,恰好满足
的正切值,小明在点阵中找到了点E,连接AE,恰好满足 于F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
于F,再作出点阵中的其它线段,就可以构造相似三角形,经过推理和计算能够使问题得到解决.
请你帮小明计算:OC=_______________; =_______________;
=_______________;
在平面直角坐标系 中,反比例函数
中,反比例函数 的图象经过点
的图象经过点 ,
,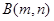 .
.
(1)求代数式mn的值;
(2)若二次函数 的图象经过点B,求代数式
的图象经过点B,求代数式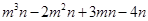 的值;
的值;
(3)若反比例函数 的图象与二次函数
的图象与二次函数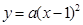 的图象只有一个交点,且该交点在直线
的图象只有一个交点,且该交点在直线 的下方,结合函数图象,求
的下方,结合函数图象,求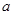 的取值范围.
的取值范围.
如图1,在△ABC 中,BC=4,以线段AB为边作△ABD,使得AD=BD, 连接DC,再以DC为边作△CDE,使得DC = DE,∠CDE=∠ADB=α.
(1)如图2 ,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3, 求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).

在平面直角坐标系xOy中,设点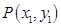 ,
, 是图形W上的任意两点.
是图形W上的任意两点.
定义图形W的测度面积:若 的最大值为m,
的最大值为m, 的最大值为n,则
的最大值为n,则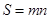 为图形W的测度面积.
为图形W的测度面积.
例如,若图形W是半径为1的⊙O.当P,Q分别是⊙O与x轴的交点时,如图1, 取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,
取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2, 取得最大值,且最大值n=2.则图形W的测度面积
取得最大值,且最大值n=2.则图形W的测度面积 .
.
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
②如图4,当AB⊥x轴时,它的测度面积S= ;
(2)若图形W是一个边长为1的正方形ABCD,则此图形测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
 ,则
,则 的值为( )
的值为( )




 与直线
与直线 的两个交点坐标分别为
的两个交点坐标分别为 ,
, ,则关于x的方程
,则关于x的方程 的解为__________.
的解为__________.
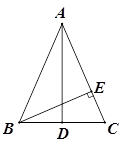
 .
.
 是一元二次方程
是一元二次方程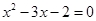 的实数根,求代数式
的实数根,求代数式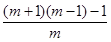 的值.
的值. 平移后经过点
平移后经过点 ,
, ,求平移后的抛物线的表达式.
,求平移后的抛物线的表达式. 有两个不相等的实数根
有两个不相等的实数根 ,
, .
. ,且
,且 ,求整数m的值.
,求整数m的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号