暖春三月,贴心开学测 初二数学第六套
下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
| A.3cm,4cm,8cm | B.cm,7cm,15cm |
| C.13cm,12cm,20cm | D.5cm,5cm,11cm |
已知一次函数y=kx﹣k,若y随x的减小而减小,则该函数的图象经过第( )象限.
| A.一、二、三 | B.一、二、四 |
| C.一、三、四 | D.二、三、四 |
如图,AE∥FD,AE=FD,要使△EAC≌△FDB,需要添加下列选项中的( )

| A.AB=BC | B.EC=BF | C.∠A=∠D | D.AB=CD |
如图所示,在3×3的正方形网格中已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的办法有( )

| A.3种 | B.4种 | C.5种 | D.6种 |
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用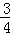 h,立即按原路以另一速度返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示,现有以下4个结论:
h,立即按原路以另一速度返回,直至与货车相遇.已知货车的速度为60km/h,两车之间的距离y(km)与货车行驶时间x(h)之间的函数图象如图所示,现有以下4个结论:

①快递车到达乙地时两车相距120km;
②甲、乙两地之间的距离为300km;
③快递车从甲地到乙地的速度为100km/h;
④图中点B的坐标为(3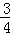 ,75).
,75).
其中,正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在Rt△ABC中,∠ABC=90°,过点B作BE⊥AC,又ED⊥BC于点D,添加一个条件,使得△ABC≌BDE.你添加的条件是 .

如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A,B,C,D的面积和是49cm2,则其中最大的正方形S的边长为 cm.

在平面直角坐标系中,规定把一个正方形先沿着x轴翻折,再向右平移2个单位称为1次变换.如图,已知正方形ABCD的顶点A、B的坐标分别是(﹣1,﹣1)、(﹣3,﹣1),把正方形ABCD经过连续7次这样的变换得到正方形A′B′C′D′,则B的对应点B′的坐标是 .

观察下列各式:
3×5=15=42﹣1
5×7=35=62﹣1
11×13=143=122﹣1
…
根据你的观察、归纳、猜想,请将你发现的规律,用只含一个字母n的式子表示出来,并予以证明.
如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.
(1)试说明:∠AEQ=90°;
(2)猜想EF与图中哪条线段相等(不能添加辅助线产生新的线段),并说明理由.
 的值为0,则x的值是( )
的值为0,则x的值是( ) = .
= . ﹣
﹣ = .
= . 的值为零,则x= .
的值为零,则x= . 和
和 是同类根式,那么,b= .
是同类根式,那么,b= . ﹣π)0+(
﹣π)0+( )﹣1+(﹣1)2.
)﹣1+(﹣1)2. ,然后从﹣2≤x≤2的范围内选取一个合适的整数作为x的值代入求值.
,然后从﹣2≤x≤2的范围内选取一个合适的整数作为x的值代入求值. +
+ )÷
)÷ ,其中m=
,其中m= .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号