暖春三月,贴心开学测 初二数学第二套
有两根木棒长度分别为3cm和4cm,若再选一根木棒使三根木棒首尾顺次相接组成一个直角三角形,则这根木棒的长度可以是( )
| A.2cm | B.3cm | C.4cm | D.5cm |
下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
| A.3cm,4cm,8cm | B.8cm,7cm,15cm |
| C.13cm,12cm,20cm | D.5cm,5cm,11cm |
下列式子一定成立的是( )
| A.a+2a2=3a3 | B.a2•a3=a6 | C.(a3)2=a6 | D.a6÷a2=a3 |
下列各式中,从左到右的变形是因式分解的是( )
| A.3x+3y﹣5=3(x+y)﹣5 |
| B.(x+1)(x﹣1)=x2﹣1 |
| C.4x2+4x=4x(x+1) |
| D.6x7=3x2•2x5 |
用一条长为16cm的细绳围成一个等腰三角形,若其中有一边的长为4cm,则该等腰三角形的腰长为( )
| A.4cm | B.6cm | C.4cm或6cm | D.4cm或8cm |
某电视台“走基层”栏目的一位记者乘汽车赴320km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是( )
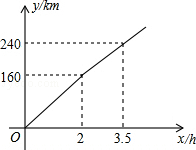
| A.汽车在高速公路上的行驶速度为100km/h |
| B.乡村公路总长为90km |
| C.汽车在乡村公路上的行驶速度为60km/h |
| D.该记者在出发后5h到达采访地 |
平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
| A.4个 | B.8个 | C.10个 | D.12个 |
一副分别含有30°和45°的两个直角三角板,拼成如图图形,其中∠C=90°,∠B=45°,∠E=30°.则∠BFD的度数是 .

在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图),把余下的部分拼成一个矩形(如图),根据两个图形中阴影部分的面积相等,可以验证的乘法公式是 .

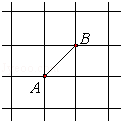
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C有 个.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
(1)求∠ECD的度数;
(2)若CE=5,求BC长.
已知:如图,△ABC中,AD⊥BC于点D,AD=DC,∠FCD=∠BAD,点F在AD上,BF的延长线交AC于点E.
(1)求证:△ABD≌△CFD.
(2)求证:BE⊥AC;
(3)设CE的长为m,用含m的代数式表示AC+BF.
如图,在△MPN中,MP=NP,∠MPN=90°,S、P、Q在同一条直线上,NQ⊥PQ,MS⊥PS,垂足分别为Q、S,QS=8.4cm,NQ=2.1cm.试求出MS的长为多少cm.
甲、乙两车分别从相距200千米的A、B两地同时出发相向而行,甲到B地后立即返回,乙到A地后停止行驶,下图是它们离各自出发地的距离y(km)与行驶时间x(h)之间的函数图象.
(1)请直接写出甲离出发地A的距离y(km)与行驶时间x(h)之间的函数关系式,并写出自变量x的取值范围;
(2)求出函数图象交点M的坐标并指出该点坐标的实际意义;
(3)求甲、乙两车从各自出发地驶出后经过多长时间相遇.


 = .
= .
 ﹣
﹣ =1.
=1.

 粤公网安备 44130202000953号
粤公网安备 44130202000953号