安徽省江淮名校高三第二次联考理科数学试卷
已知等差数列{an}的前n项之和是Sn,则-am<a1<-am+l是Sm>0,Sm+1<0的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充分必要条件 |
| D.既不充分也不毖要 |
若非零向量 ,满足
,满足 ,则( )
,则( )
A.|2  |>|2 |>|2  + +  | | |
B.|2  |<|2 |<|2  + +  | | |
C.|2  |>| |>| + +  | | |
D.|2  |<| |<| + +  | | |
已知函数 ,的零点
,的零点 ,其中常数a,b满足2a =3,3b =2,则n的值是( )
,其中常数a,b满足2a =3,3b =2,则n的值是( )
| A.-2 | B.-l | C.0 | D.1 |
已知数列{an}的前n项之和是Sn,且4Sn=(an+1)2,则下列说法正确的是
| A.数列{an}为等差数列 |
| B.数列{an}为等差或等比数列 |
| C.数列{an}为等比数列 |
| D.数列{an}可能既不是等差数列也不是等比数列 |
如图,在第一象限内,矩形ABCD的三个顶点A,B,C分别在函数y=lo ,的图像上,且矩形的边分别平行两坐标轴,若A点的纵坐标是2,则D点的坐标是 。
,的图像上,且矩形的边分别平行两坐标轴,若A点的纵坐标是2,则D点的坐标是 。
已知正项等比数列{an}满足a2015=2a2013+a2014,若存在两项am、an使得 则
则 的最小值为 .
的最小值为 .
若正实数a使得不等式|2x - a|+|3x- 2a|≥a2对任意实数x恒成立,则实数a的范围是 。
已知集合M=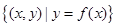 ,对于任意实数对
,对于任意实数对 ,存在实数对(x1,y2)
,存在实数对(x1,y2)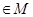 使得x1x2+y1y2=0成立,则称集命M是:“孪生对点集”-给出下列五个集合-;
使得x1x2+y1y2=0成立,则称集命M是:“孪生对点集”-给出下列五个集合-;
①
②
③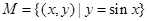
④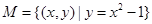
⑤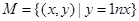
其中不是“孪生对点集”的序号是 。
(本小题满分12分)已知函数 在区间[2,3]上有最大值4和最小值1.设
在区间[2,3]上有最大值4和最小值1.设 .
.
(1)求a、b的值;
(2)若不等式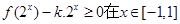 上有解,求实数k的取值范围。
上有解,求实数k的取值范围。
(本小题满分l2分)已知{an}的前n项和 (其中
(其中 ),且Sn的最大值为9。
),且Sn的最大值为9。
(1)确定常数k的值,并求数列{an}的通项公式;
(2)求数列 的前n项和
的前n项和 。
。
(本小题满分12分)利用已学知识证明:
(1)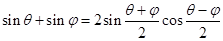 。
。
(2)已知△ABC的外接圆的半径为2,内角A,B,C满足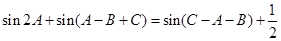 ,求△ABC的面积。
,求△ABC的面积。
(本小题满分12分)合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50 米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.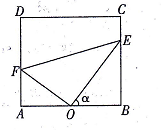
(1)设∠BOE=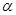 ,试将△OEF的周长
,试将△OEF的周长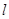 表示成
表示成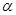 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
(本小题满分13分)已知函数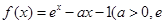 为自然对数的底数)
为自然对数的底数)
(1)求函数 的最小值;
的最小值;
(2)若 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明: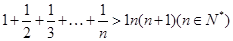
 ,则
,则 =( )
=( ) 在复平面内对应的点位于( )
在复平面内对应的点位于( )




 ,若
,若 ,则实数
,则实数 的值为
的值为



 +x0-2014>0”的否定是
+x0-2014>0”的否定是  且a1=3。
且a1=3。 满足
满足 ,Sn为数列
,Sn为数列 。
。 粤公网安备 44130202000953号
粤公网安备 44130202000953号