江苏省江阴市青阳片九年级上学期期中考试数学试卷
下列线段能构成比例线段的是 ( )
| A.1,2,3,4 |
B.1, , , ,2 ,2 |
C. , , , , ,1 ,1 |
| D.2, 5, 3, 4 |
一元二次方程 根的情况是 ( )
根的情况是 ( )
| A.有两个不相等的实数根 |
| B.有两个相等的实数根 |
| C.无实数根 |
| D.无法确定 |
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A. |
B. |
C. |
D. |
某商品原价500元,连续两次降价 后售价为200元, 下列所列方程正确的是( )
后售价为200元, 下列所列方程正确的是( )
A. |
B. |
C. |
D. |
下列说法不正确的是( )
| A.半圆(或直径)所对的圆周角是直角 |
| B.等边三角形的重心与外心重合 |
| C.相等的弧所对的圆心角相等 |
| D.平分弦的直径垂直于弦 |
如图,在平面直角坐标系中,过格点A、B、C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )
A.点(0,3) B.点(2,3) C.点(5,1) D.点(6,1)
如图,已知矩形ABCD∽矩形ECDF,且AB=BE,那么BC与AB的比值是( )
A. |
B. |
C. |
D. |
李老师从“淋浴龙头”受到启发.编了一个题目:
在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A,B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM与x轴交于点N(n,0),如图3.当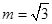 时,求n的值.你解答这个题目得到的n值为( )
时,求n的值.你解答这个题目得到的n值为( )
A. |
B.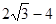 |
C.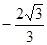 |
D.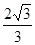 |
在比例尺为1∶2000000的地图上,量得M、N两地的距离为2.5cm,则这两地间的实际距离为____千米.
给出下列几何图形:①两个圆;②两个正方形;③两个矩形;④两个正六边形;⑤两个等边三角形;⑥两个直角三角形;⑦两个菱形.其中,一定相似的有_ _(填序号).
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于 .
如图,已知AB是半圆的直径,且AB=10,弦AC=6,将半圆沿过点A的直线折叠,使点C落在直径AB上的点C′,则折痕AD的长为 .
在等腰△ABC中,三边分别为a、b、c,其中 ,若关于x的方程
,若关于x的方程 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
配方法可以用来解一元二次方程,还可以用它来解决很多问题.例如:因为 ,所以
,所以 ,即:
,即: 有最小值1,此时
有最小值1,此时 ;同样,因为
;同样,因为 ,所以
,所以 ,即
,即 有最大值6,此时
有最大值6,此时  .
.
(1)当 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(2)当 = 时,代数式
= 时,代数式 有最 (填写大或小)值为 .
有最 (填写大或小)值为 .
(3)矩形花园的一面靠墙,另外三面的栅栏所围成的总长度是16m,当花园与墙相邻的边长为多少时,花园的面积最大?最大面积是多少?
已知在△ABC中,AB= ,AC=
,AC= ,BC=3.
,BC=3.
(1)如图,点M为AB的中点,在线段AC上取点N,使△AMN与△ABC相似,求线段MN的长;
(2)如图,是由100个边长为1的小正方形组成的10×10的正方形网格, 设顶点在这些小正方形顶点的三角形为格点三角形.
①请你在所给的网格中画出格点△A1B1C1与△ABC全等(画出一个即可,不需证明);
②试直接写出所给的网格中与△ABC相似且面积最大的格点三角形的个数,并画出其中一个(不需证明).
某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若 ,求
,求 的值.
的值.
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 , 的值是 .
的值是 .
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是 (用含
的值是 (用含 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若 ,则
,则 的值是 (用a,b含的代数式表示).
的值是 (用a,b含的代数式表示).
如图,在平面直角系中,点A、B分别在x轴、y轴上,A(8,0),B(0,6),点P从点B出发,沿BA以每秒1个单位的速度向点A运动,点Q从点A出发,沿AO以每秒1个单位的速度向点O运动,当点Q到达点O时,两点同时停止运动,设点Q的运动时间为t秒.
(1)用含t的代数式表示C点坐标;
(2)如图1,连接PQ,过点Q作QC⊥AO交AB于点C,在整个运动过程中,当t为何值时,△CPQ为等腰三角形?
(3)如图2,以QC为直径作⊙D,⊙D与AB的另一个公共点为E.问是否存在某一时刻t,使得以BC、CE、AE的长为边的三角形为直角三角形?若存在,直接写出一个符合题意的t的值;若不存在,请说明理由.
 ②
② ③
③ ④
④ 
 ,
, 是方程
是方程 的两个根,则
的两个根,则 的值为( )
的值为( )

 是方程
是方程 的一个根,则方程另一根为 .
的一个根,则方程另一根为 .

 (配方法)
(配方法)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号