湖北省通山县九年级上学期期中考试数学试卷
如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是 ( )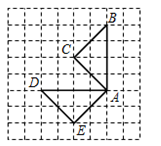
| A.顺时针旋转90° | B.逆时针旋转90° |
| C.顺时针旋转45° | D.逆时针旋转45° |
抛物线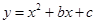 的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为
的图象先向右平移2个单位,再向下平移3个单位,所得图象的函数解析式为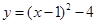 则b,c的值为( )
则b,c的值为( )
| A.b=2,c=0 |
| B.b=2,c=-6 |
| C.b=-6,c=8 |
| D.b=-6,c=2 |
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.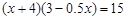 |
B.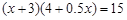 |
C.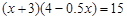 |
D.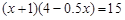 |
对抛物线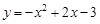 而言,下列结论正确的是( )
而言,下列结论正确的是( )
| A.与x轴有两个交点 |
| B.开口向上 |
| C.与y轴的交点坐标是(0,3) |
| D.顶点坐标是(1,-2) |
二次函数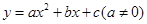 的图象如图,
的图象如图,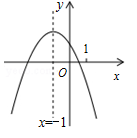
给出下列四个结论:
①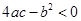 ;
;
②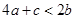 ;
;
③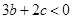 ;
;
④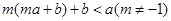 ,
,
其中正确结论的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是 .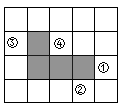
现定义运算“★”,对于任意实数a,b,都有a★b=a2-3a+b,如:3★5=32-3×3+5,若x★2=6则实数x的值是 .
在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=5,BD=4.则下列四个结论:①AE∥BC;②∠ADE=∠BDC;③△BDE是等边三角形;④△ADE的周长是9.其中正确的结论是 (把你认为正确结论的序号都填上).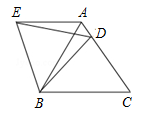
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.6万元,设可变成本平均的每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元.
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年增长的百分率x.
如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(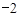 ,2),B(0,5),C(0,2).
,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(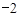 ,
,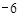 ),请画出平移后对应的△A2B2C2的图形.
),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
已知一元二次方程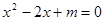 .
.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为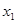 ,
,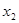 ,且
,且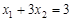 ,求m的值.
,求m的值.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC交AC于点E,点D在AB上,DE⊥EB.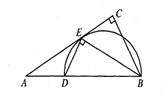
(1)求证:AC是△BDE的外接圆的切线;
(2)若AD=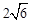 ,AE=
,AE=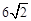 ,求EC的长.
,求EC的长.
如图,利用一面墙(墙的长度为20m),用34m长的篱笆围成两个鸡场,中间用一道篱笆隔开,每个鸡场均留一道1m宽的门,设AB的长为x m.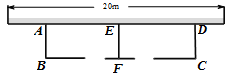
(1)若两个鸡场总面积为96m2,求x;
(2)若两个鸡场的面积和为S m2,写出S关于x的关系式;并求当x为何值时,两个鸡场面积和最大,最大值是多少?
【操作探究】如图1,在Rt△ABC中,∠BAC=90°,AB=AC,点D,E是BC边上的任意两点,且∠DAE=45°.
(1)将△ABD绕点A逆时针旋转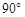 ,得到△ACF,请在图(1)中画出△ACF.
,得到△ACF,请在图(1)中画出△ACF.
(2)在(1)中,连接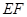 ,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.
,探究线段BD,EC和DE之间有怎样的数量关系?写出猜想,并说明理由.
【方法应用】
(3)如图2,M,N分别是正方形ABCD的边BC,CD上一点,且BM+DN=MN,试求∠MAN的大小.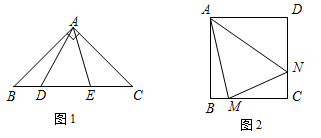

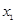 ,
,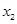 是方程
是方程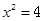 的两根,则
的两根,则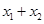 的值是( )
的值是( )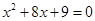 左边变成完全平方式后,方程是( )
左边变成完全平方式后,方程是( )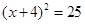

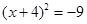
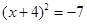
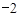 ,3)关于原点对称点的坐标为 .
,3)关于原点对称点的坐标为 .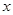 的一元二次方程的一个根是
的一元二次方程的一个根是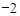 ,写出一个符合条件的方程: .
,写出一个符合条件的方程: .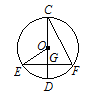
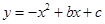 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表: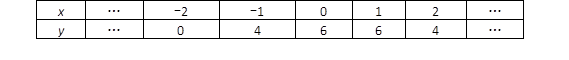
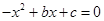 的两个根为 .
的两个根为 .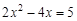 .
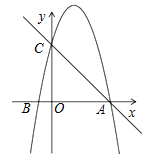
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号