江苏省扬州市邗江区八年级上学期期中测试数学试卷
下列说法中,正确的是( )
| A.两个全等三角形一定关于某直线对称 |
| B.等边三角形的高、中线、角平分线都是它的对称轴 |
| C.两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧 |
| D.关于某直线对称的两个图形是全等形 |
等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )
| A.16 | B.18 | C.20 | D.16或20 |
如图,△ABC≌△DEF,BE=4,则AD的长是( )
| A.5 | B.4 | C.3 | D.2 |
如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
| A.BC=EC,∠B=∠E |
| B.BC=EC,AC=DC |
| C.AC=DC,∠B=∠E |
| D.∠B=∠E,∠BCE=∠ACD |
由下列条件不能判定△ABC为直角三角形的是( )
| A.∠A+∠B=∠C |
| B.∠A:∠B:∠C =1:3:2 |
| C.(b+c)(b-c)=a2 |
D.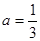 , ,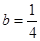 , ,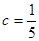 |
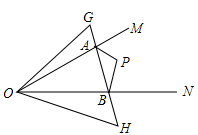
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H, GH分别交OM、ON于A、B点,若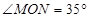 ,则
,则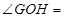 ( )
( )
A.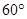 B.
B.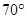 C.
C.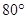 D.
D.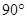
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.则当PB+PE的值为最小值时,点P的位置在( ).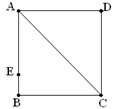
| A.AC的三等分点 | B.AC的中点 |
| C.连接DE与AC的交点 | D.以上答案都不对 |
当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”。如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为___________度。
如图,∠A=36°,∠DBC=36°,∠C=72°,则图中等腰三角形有_____________个。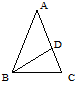
如图,△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为____________cm。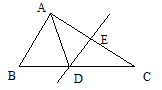
如图,是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是___________________ 。
如图,由四个直角边分别为3和4全等的直角三角形拼成“赵爽弦图”,其中阴影部分面积为______________。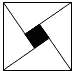
如图,每个小正方形的边长为1,A,B,C是小正方形的顶点,则∠ABC的度数为________________。
如图,△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为 _____________。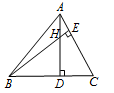
如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需__________cm.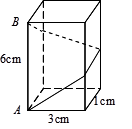
等腰三角形的底边长为10cm,一腰上的中线把这个三角形的周长分成两个部分的差为3cm,则腰长为_____________________cm 。
如下图,有公路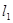 同侧、
同侧、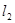 异侧的两个城镇A、B,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路
异侧的两个城镇A、B,电信部门要修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离必须相等,到两条公路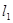 、
、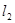 的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)
的距离也必须相等,发射塔C应修建在什么位置?请用尺规作图找出所有符合条件的点,注明点C的位置。(保留作图痕迹,不写作法)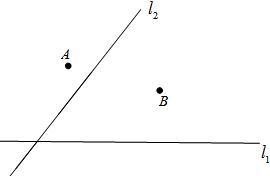
如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上. 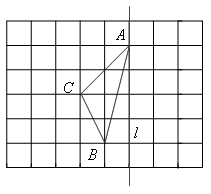
(1) 在图中画出与关于直线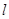 成轴对称的△A'B'C';
成轴对称的△A'B'C';
(2) 线段CC'被直线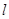 ;
;
(3)△ABC的面积为_______________;
已知:如图,点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.
求证:(1)△ABC≌△DEF;(2)BE=CF.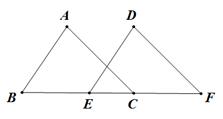
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
(1)折叠后,DC的对应线段是 ,
(2)若∠1=60°,求∠3的度数;
(3)若AB=4,AD=8,求BE的长度.
如图,已知△ABC是等边三角形,点D、E分别在AC、BC上,且CD=BE,求:∠AFD的度数?.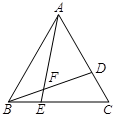
如图,在△ABC中,AB=13,BC=10, BC边上的中线AD=12.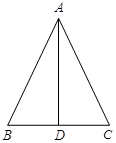
(1)AD平分∠BAC吗?请说明理由.
(2)求:△ABC的面积.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF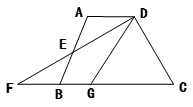
(1)求证:△ADE≌△BFE。
(2)连接EG,判断EG与DF的位置关系并说明理由。
△ABC中,∠C=90°,AC=3,BC=4,在BC边上找一点P,使得点P到点C的距离与点P到边AB的距离相等,求BP的长.
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:(1) ;(2)
;(2)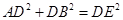

 粤公网安备 44130202000953号
粤公网安备 44130202000953号