针对生活中的一些物理量的估测,下列合理的是( )
| A. |
课桌的高度为1.6m |
| B. |
中学生百米跑平均速度为7.1m/s |
| C. |
人体的体积为0.5m 3 |
| D. |
温暖舒适的气温为37℃ |
如图,当溢水杯盛满某种液体时,把实心物块缓慢放入杯中,物块漂浮,静止后溢出液体的质量为m 1;当溢水杯盛满密度为ρ的液体时,把同一物块缓慢放入杯中,物块沉底,静止后溢出液体的质量为m 2.则物块的密度为 。
空气的成分按体积计算,氮气约占78%,氧气约占21%,根据下表中一些气体密度估算你所在教室里空气的质量,合理的是( )
一些气体的密度(0℃,标准大气压)
| 物质 |
氮气 |
氧气 |
二氧化碳 |
氢气 |
| 密度/(kg•m ﹣ 3) |
1.25 |
1.43 |
1.98 |
0.09 |
| A. |
20kg |
B. |
200kg |
C. |
1000kg |
D. |
2.0×10 5kg |
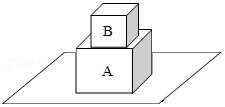
如图所示,有两个正方体实心物体A、B叠放在水平桌面上,物体A重15N,B重5N.若物体B对A的压强与此时物体A对桌面的压强相等。则物体B对A的压力与物体A对桌面的压力之比是 ,物体B与A的密度之比是 。
如图所示是甲和乙两种物质的质量和体积关系图象,下列说法正确的是
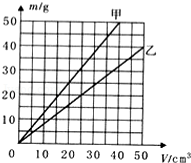
A.乙物质的密度比水大
B.体积为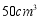 的乙物质的质量为
的乙物质的质量为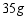
C.质量为 的甲物质的体积为
的甲物质的体积为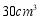
D.当甲和乙两物质的质量相同时,乙物质的体积较大
利用材料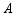 制造强力磁铁。
制造强力磁铁。
(1)加热材料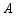 ,温度一直低于其熔点,一段时间后,
,温度一直低于其熔点,一段时间后, 质量不变、体积减小,此过程中,
质量不变、体积减小,此过程中,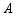 处于 (选填“固态”、“液态”、“固液混合态”
处于 (选填“固态”、“液态”、“固液混合态”  ,依据公式 ,
,依据公式 ,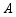 的密度 (选填“增大”、“减小”、“不变”
的密度 (选填“增大”、“减小”、“不变”  。
。
(2)如图1所示, 的每个原子都有
的每个原子都有 、
、 极,相当于磁性很弱的“小磁铁”,“小磁铁”杂乱无章排列时,
极,相当于磁性很弱的“小磁铁”,“小磁铁”杂乱无章排列时, 对外不显磁性,当“小磁铁”按图2所示同向排列时,
对外不显磁性,当“小磁铁”按图2所示同向排列时, 具有磁性(如图
具有磁性(如图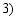 ,强力磁铁不耐高温,高温加热会使磁性消失,从分子热运动的角度解释为什么高温会让强力磁铁磁性消失, 。
,强力磁铁不耐高温,高温加热会使磁性消失,从分子热运动的角度解释为什么高温会让强力磁铁磁性消失, 。

正方体塑料块A边长lA=0.1m,它所受的重力GA=6N.另一圆柱体B高hB=0.1m,底面积SB=5×10﹣3m2,它的密度ρB=1.6×103kg/m3.已知水的密度ρ水=1.0×103kg/m3,取g=10N/kg。
(1)圆柱体B所受的重力是多少?
(2)将塑料块A浸没在水中,通过计算说明释放后它上浮还是下沉?
(3)如图所示,将圆柱体B置于塑料块A正上方,放入一个水平放置的水槽中,向水槽缓慢注水,请写出塑料块A对水槽底部的压强p。

从冰箱里取出一袋冰块,过一段时间后,冰块全部化成水。则冰块熔化成水后,下列说法正确的是( )
A.质量变大,密度变小B.质量变小,密度变大
C.质量不变,密度变大D.质量不变,密度不变
一种有防干烧功能的养生壶,如图所示,其相关参数如下表,用该养生壶烧水,壶内的水少于容量的四分之一时自动断电。为使该壶能通电烧水,壶内至少加入 kg的水;假如水的初温为20℃,已知水的比热容c水=4.2×103J/(kg•℃),则使用该壶将1kg的水加热到100℃,水所吸收的热量是 J;在加热水的过程中部分热量损失了,其原因是 (列举一个原因即可)。
型号 |
电源 |
额定功率 |
容量 |
21A213 |
220V﹣50Hz |
400W |
2000mL |

把一杯水放入冰箱的冷冻室中,当水结成冰后密度 ,体积 (选填“变大”“不变”或“变小”)。
如图是某品牌饮水机的简化电路图,该饮水机有加热和保温两种工作状态(由机内温控开关S0自动控制),下表是它的有关参数。已知C水=4.2×103J/(kg•℃),ρ水=1.0×103kg/m3。
电热饮水机 型号:XL﹣LS2017 储水罐容积:1L 额定电压:220V 额定加热功率:1000W 额定保温功率:100W 额定频率:50Hz |
(1)S0闭合时饮水机处于什么状态,此时电路中电流是多大?
(2)该饮水机在额定电压下,将装满储水罐的水从50℃加热至沸腾(当时气压为标准大气压),用时300s,求饮水机的加热效率。
(3)若实际电压为200V,饮水机的加热效率保持不变,将装满储水罐的水从50℃加热至沸腾(当时大气压为标准大气压),需用时多少秒。

小明同学阅读了下表后,归纳了一些结论,其中正确的是
0℃,1标准大气压下部分物质的密度(kg/m3) |
|||
煤油 |
0.8×103 |
干松木 |
0.4×103 |
酒精 |
0.8×103 |
冰 |
0.9×103 |
水 |
1.0×103 |
铝 |
2.7×103 |
水银 |
13.6×103 |
铜 |
8.9×103 |
( )
A.同种物质的密度一定相同
B.不同物质的密度一定不同
C.固体物质的密度一定比液体物质的密度大
D.相同质量的实心铜块和铝块,铜块的体积较小
如图为一健身器材模型,杠杆AB可绕O点在竖起平面内转动,OA:OB=1:4,质量为60kg的小明站在水平放置的体重计上,通过该杠杆提起吊篮中的重物,吊篮重80N,当边长为20cm的正方体重物甲刚被提起时,体重计示数为43kg。当边长为40cm的正方体重物乙刚被提起时,体重计示数为18kg。杠杆始终在水平位置保持平衡,A、B两端绳子拉力保持竖直,不计绳重、杠杆自重及摩擦,g取10N/kg,则重物甲与重物乙的密度之比为( )
A.1:3B.2:3C.3:2D.3:1
如图所示,两根完全相同的轻细弹簧,原长均为L0=20cm,甲图中长方体木块被弹簧拉着浸没在水中,乙图中长方体石块被弹簧拉着浸没在水中。木块和石块体积相同,木块和石块静止时两弹簧长度均为L=30cm。已知,木块重力G木=10N,水和木块密度关系ρ水=2ρ木,ρ水=1×103kg/m3(忽略弹簧所受浮力)。
(1)求甲图中木块所受浮力;
(2)若弹簧的弹力满足规律:F=k(L﹣L0),求k值(包括数值和单位);
(3)求石块的密度。
