初中数学三角形的五心试题

如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（   ）

A．CB=CD	B．∠BAC=∠DAC
C．∠BCA=∠DCA	D．∠B=∠D=90°

已知: 如图, AC、BD相交于点O, ∠A =∠D, 请你再补充一个条件, 使△AOB≌△DOC, 你补充的条件是 _______________ 。

如图，△ABC中，DE∥BC，DE=1，AD=2，DB=3，则BC的长是（     ）

A．

B．

C．

D．

不能确定△ABC与△DEF全等的是（   ）。

A．AC=DF，AB=DE，BC=EF,	B．AB=DE，∠A=∠D， BC=EF
C．AC= DF，∠A=∠D，∠C=∠F	D．AC= DF，∠B=∠E，∠A=∠D

如图，在△ABC中，AB=BC，∠ABC=90°，BM是AC边中线，点D，E分别在边AC和BC上，DB=DE，EF⊥AC于点F，以下结论：
（1）∠DBM=∠CDE；
（2）S_△BDE＜S_{四边形BMFE}；
（3）CD•EN=BN•BD；
（4）AC=2DF．
其中正确结论的个数是（ ）．

A．1

B．2

C．3

D．4

如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使CD=BC，再定出BF的垂线DE，使A、C、E在一条直线上，可以证明△EDC≌△ABC，得到ED=AB，因此测得ED的长就是AB的长（如图），判定△EDC≌△ABC的理由是（   ）

A．SAS      B．ASA；   C．SSS     D．HL

直角三角形两直角边长分别为3和4，则它斜边上的高是（ ）

A．3.5

B．2.4

C．1.2

D．5

已知△ABC与△DEF的三边对应相等，三个角也对应相等，则能判定△ABC与△DEF全等的方法有（ ）种．

A．13

B．12

C．11

D．10

在△ABC中和△DEF中，已知AC=DF，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF的是（   ）

A．BC=EF

B．AB=DE

C．∠A=∠D

D．∠B=∠E

一个等腰三角形的两边长分别是4和9，则它的周长为（ ）

A．17

B．20

C．22

D．17或22

如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（  ）

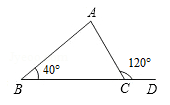
A．60°

B．70°

C．80°

D．90°

如图，在△ABC中，AC＝BC，∠ACB＝90°，AE平分∠BAC交BC于E，BD⊥AE于D，DF⊥AC交AC的延长线于F，连接CD，给出三个结论：

①AE＝2BD；   ②AB－AC＝CE；  ③CE＝2FC；
其中正确的结论有（   ）．

A．0个

B．1个

C．2个

D．3个

下列三条线段不能构成直角三角形的是（  ）

A．1、、2

B．、、

C．5、12、13

D．9、40、41

如图，在四边形ABCD中，AB∥CD，连接BD．请添加一个适当的条件             ，使△ABD≌△CDB．（只需写一个）

如图所示，△ABC为等腰三角形，AB=AC且AD⊥BC，垂足为D，求证：△ABD≌△ACD。