初中数学三角形的五心试题

如图，AB∥CD，AB=CD，点E、F在AD上，且AE=DF．
求证：△ABE≌△DCF．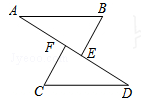

已知等腰三角形两边长是8cm和4cm，那么它的周长是（   ）

A．12cm

B．16cm

C．16cm或20cm

D．20cm

△ABC中，∠A=30°，当∠B=_________     时，△ABC是等腰三角形．

一个多边形的每个内角都等于144°，则这个多边形的边数是      ( ▲ )

A．8

B．9

C．10

D．11

如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连接BF，CE、下列说法：①CE=BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（ ）

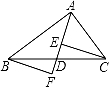
A．1个

B．2个

C．3个

D．4个

如图，在△ABC中，点D是BC延长线上一点，∠B =40°，∠ACD=120°， 则∠A等于（   ）

A． 60°      B．70°  C．80°    90°

直角三角形两直角边长分别为3和4，则它斜边上的高是（ ）

A．3.5

B．2.4

C．1.2

D．5

已知△ABC与△DEF的三边对应相等，三个角也对应相等，则能判定△ABC与△DEF全等的方法有（ ）种．

A．13

B．12

C．11

D．10

在△ABC中和△DEF中，已知AC=DF，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF的是（   ）

A．BC=EF

B．AB=DE

C．∠A=∠D

D．∠B=∠E

一个等腰三角形的两边长分别是4和9，则它的周长为（ ）

A．17

B．20

C．22

D．17或22

如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（  ）

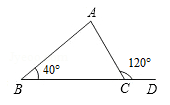
A．60°

B．70°

C．80°

D．90°

如图，在△ABC中，AC＝BC，∠ACB＝90°，AE平分∠BAC交BC于E，BD⊥AE于D，DF⊥AC交AC的延长线于F，连接CD，给出三个结论：

①AE＝2BD；   ②AB－AC＝CE；  ③CE＝2FC；
其中正确的结论有（   ）．

A．0个

B．1个

C．2个

D．3个

下列三条线段不能构成直角三角形的是（  ）

A．1、、2

B．、、

C．5、12、13

D．9、40、41

如图，在四边形ABCD中，AB∥CD，连接BD．请添加一个适当的条件             ，使△ABD≌△CDB．（只需写一个）

如图所示，△ABC为等腰三角形，AB=AC且AD⊥BC，垂足为D，求证：△ABD≌△ACD。