二次函数y=x2的图象向上平移2个单位,得到新的图象的二次函数表达式是( )
| A.y=x2-2 | B.y=(x-2)2 | C.y=x2+2 | D.y=(x+2)2 |
请写出一个开口向下,并且与y轴交于点(0,-2)的抛物线的表达式__________.
二次函数 的图象如图所示,则下列结论中错误的是( )
的图象如图所示,则下列结论中错误的是( )
| A.函数有最小值 |
B.当 时, 时, |
C. |
D.当 ,y随x的增大而减小 ,y随x的增大而减小 |
如图1,对于平面上不大于 的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为
的∠MON,我们给出如下定义:若点P在∠MON的内部或边界上,作PE⊥OM于点E,PF⊥ON于点F,则称PE+PF为点P相对于∠MON的“点角距离”,记为 .
.
如图2,在平面直角坐标系xOy中,对于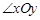 ,点P为第一象限内或两条坐标轴正半轴上的动点,且满足
,点P为第一象限内或两条坐标轴正半轴上的动点,且满足 5,点P运动形成的图形记为图形G.
5,点P运动形成的图形记为图形G.
(1)满足条件的其中一个点P的坐标是 ,图形G与坐标轴围成图形的面积等于 ;
(2)设图形G与x轴的公共点为点A,已知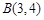 ,
, ,求
,求 的值;
的值;
(3)如果抛物线 经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当
经过(2)中的A,B两点,点Q在A,B两点之间的抛物线上(点Q可与A,B两点重合),求当 取最大值时,点Q 的坐标.
取最大值时,点Q 的坐标.
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
| A.16 | B.15 | C.14 | D.13 |
把抛物线 向右平移3个单位,再向下平移2个单位,得到抛物线( )
向右平移3个单位,再向下平移2个单位,得到抛物线( )
A. |
B. |
C. |
D. |
二次函数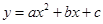 的部分对应值如下表:
的部分对应值如下表:
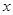 |
… |
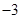 |
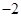 |
 |
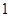 |
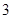 |
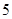 |
… |
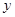 [m] [m] |
… |
7 |
0 |
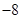 |
-9 |
-5 |
7 |
… |
下面关于二次函数及其图象说法不正确的是( )
A.对称轴为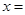 1
1
B.y的最大值是-9
C.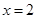 对应的函数值
对应的函数值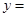 -8
-8
D.抛物线截x轴所得的线段长是6
二次函数 的图像上有点A(2013,a),B (2014,b),关于a,b的大小关系,下列正确的是( )
的图像上有点A(2013,a),B (2014,b),关于a,b的大小关系,下列正确的是( )
| A.a>b |
| B.a<b |
| C.a=b |
| D.m的取值不确定,无法确定a,b的大小 |
二次函数y =ax2+bx+c的图象的形状 ( )
| A.只与a有关 | B.只与b有关 | C.只与a, b有关 | D.与 a , b,c都有关 |
如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.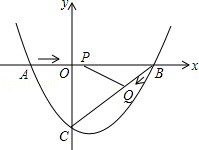
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.