小学数学圆、圆环的周长试题

求阴影部分面积．（单位：厘米）

在一个长10dm，宽7dm的硬纸板里剪半径是3dm的圆，可剪（　　）个．
A．1      B．2       C．3

已知半圆的半径是r，则计算它的周长算式是（　　）

A．πr

B．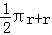

C．πr+r

D．πr+2r

一张光盘的刻录面为环形，内圆的直径是4厘米，外圆直径是12厘米，这张光盘刻录面的面积是　　　　　　平方厘米．

一种玩具车车轮的半径是3厘米，它在路面上滚动一周，滚动了　　　　　　厘米．

画一个周长是25.12厘米的圆，圆规两脚尖的距离是　　　　　　厘米，面积是　　　　　　平方厘米．

从一个边长是10分米的正方形纸里剪一个最大的圆，这个圆的周长是　　　　　　分米，面积是　　　　　　平方分米．

求阴影部分的面积．（单位：cm）

一张圆形的纸，至少要对折（　　）次，才能看到圆心．
A．1次  B．2次  C．3 次

周长相等的两个圆，它们的面积也一定相等．　　　　　　．（判断对错）

在一个长12厘米，宽10厘米的长方形内画一个最大的圆，这个圆的面积是　　　　　　平方厘米．

把一个圆分成若干（偶数）等份，分得越细，拼成的图形越接近于长方形，这个长方形的长相当于圆的周长的　　　　　　，长方形的宽就是圆的　　　　　　．

　　　　　　决定圆的位置，　　　　　　决定圆的大小．

请用圆规画出一个直径是6cm的圆，再在圆中画一个圆心角是100°的扇形．

我们都学习了扇形的面积，试回忆扇形面积公式的推导过程，并根据你的理解，回答下列问题．
（1）对于一个半径为r，圆心角为n°的扇形，其面积为：　　　　　　．
（2）你认为上述扇形面积公式的推导过程，与下列哪个公式的推导使用了基本相同的方法　　　　　A、圆的面积公式；  B、圆的周长公式；  C、平行四边形的面积公式；  D、弧长公式．
（3）在上述扇形面积的推导过程中，下列哪些知识起着重要的作用（有几个写几个）　　　　　　A、圆的面积公式；  B、圆的周长公式；  C、弧长公式；  D、分数的意义；  E、角的有关概念．
（4）如果已知一个扇形的弧长为l，半径为r，试用l和r表示该扇形的面积，并写出简要的推导过程．