如图所示,一质点沿半径为r=20cm的圆周自A点出发,逆时针运动2s,运动3/4圆周到达B点,则质点在这段时间内的路程为________m;位移为______m,方向是______.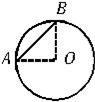
一小球从水平台面边缘以速度v水平飞出,落到水平地面上需要时间为t,落地点距台面边缘的水平距离为s.若使小球以速度2v仍从同一位置水平飞出,落到水平地面上需要时间为 ;落地点距台面边缘的水平距离为 .

下列说法正确的是 。
A.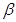 射线与 射线与 射线一样都是电磁波,但 射线一样都是电磁波,但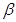 射线的穿透本领远比 射线的穿透本领远比 射线的弱 射线的弱 |
| B.玻尔将量子观念引入原子领域,其理论能够解释氢原子光谱的特征 |
| C.氢原子的核外电子由离原子核较远的轨道跃迁到离核较近的轨道上时氢原子的能量减少 |
| D.原子核中,比结合能越小,表示原子核中的核子结合得越牢固 |
E. 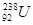 衰变成
衰变成 要经过6次
要经过6次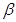 衰变和8次
衰变和8次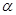 衰变
衰变
关于机械振动与机械波,下列说法正确的是 。
| A.机械波的频率等于振源的振动频率 |
| B.机械波的传播速度与振源的振动速度相等 |
| C.质点振动的方向总是垂直于波传播的方向 |
| D.在一个周期内,沿着波的传播方向,振动在介质中传播一个波长的距离 |
E. 机械波在介质中传播的速度由介质本身决定
电量为2×10﹣6C的正点电荷放入电场中A点,受到作用力为6×10﹣4 N,方向向右,则A点的场强为 N/C,方向 .若把另一电荷放在该点受到力为3×10﹣4 N,方向向左,则这个电荷的电量为 C,是 电荷.
做匀变速直线运动的质点,某阶段的初速度为v1,末速度为v2,则其在该过程的中点位置时的速度v= ;若已知该质点在另一阶段的前一半位移内平均速度为u1,后一半位移内的平均速度为u2, 则质点在此过程中间位置时的速度u= .
一个做匀加速直线运动的物体,初速度v0=2.0m/s,在第1s 内通过的位移是3m,则它的加速度为 m/s2,在最初的3s内位移为 m.
某同学在做“研究小车速度随时间变化的规律”这一实验中:该同学在小车的后面连上纸带,利用纸带上打出的点计算小车各个时刻的速度.某次打出的一条纸带如图所示.该同学已在这条纸带上取好了计数点,每两个计数点间还有4个点未画出.计数点的编号依次为:A、B、C、D、E,打点计时器的电源频率为50Hz.他把一刻度尺放在纸带上,其零刻度线和计数点A对齐.

(1)接通打点计时器电源和让纸带开始运动,这两个操作之间的时间顺序关系是 (填写序号)
A.先接通电源,后让纸带运动
B.先让纸带运动,再接通电源
C.让纸带运动的同时接通电源
D.先让纸带运动或先接通电源都可以
(2)用该刻度尺测量出计数点AB之间的距离为 cm,BC之间距离为 cm.
(3)计算打B这个计数点时小车的瞬时速度vB= m/s,小车的加速度是 m/s2.
如图甲所示,一位同学利用光电计时器等器材做“验证机械能守恒定律”的实验.有一直径为d、质量为m的金属小球由A处由静止释放,下落过程中能通过A处正下方、固定于B处的光电门,测得A、B间的距离为H(H>>d),光电计时器记录下小球通过光电门的时间为t,当地的重力加速度为g.则:
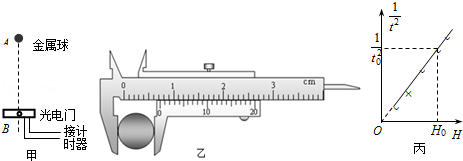
(1)如图乙所示,用游标卡尺测得小球的直径d= mm.
(2)小球经过光电门B时的速度表达式为 .
(3)多次改变高度H,重复上述实验,作出 随H的变化图象如图丙所示,当图中已知量t0、H0和重力加速度g及小球的直径d满足以下表达式: 时,可判断小球下落过程中机械能守恒.
随H的变化图象如图丙所示,当图中已知量t0、H0和重力加速度g及小球的直径d满足以下表达式: 时,可判断小球下落过程中机械能守恒.
(4)实验中发现动能增加量△EK总是稍小于重力势能减少量△EP,增加下落高度后,则△Ep﹣△Ek将 (选填“增加”、“减小”或“不变”).