用油膜法估测分子的大小.
实验器材有：浓度为0.05%(体积分数)的油酸酒精溶液、最小刻度为0.1 mL的量筒、盛有适量清水的浅盘、痱子粉、胶头滴管、玻璃板、彩笔、坐标纸(最小正方形边长为1 cm).则
(1)下面给出的实验步骤中，正确排序应为______(填序号)
为估算油酸分子的直径，请补填最后一项实验步骤D
| A．待油酸薄膜的形状稳定后，将玻璃板放在浅盘上，用彩笔将油酸薄膜的形状画在玻璃板上 |
| B．用滴管将浓度为0.05%的油酸酒精溶液一滴一滴地滴入量筒中，记下滴入1 mL油酸酒精溶液的滴数N |
| C．将痱子粉均匀地撒在浅盘内水面上，用滴管吸取浓度为0.05 %的油酸酒精溶液，从低处向水面中央滴入一滴 |
| D．_______________________________________________ |
_________________________________________________.
(2)利用以上测量数据，写出单个油酸分子直径的表达式为
___________________________________________.
关于下列四幅图的说法，正确的是 ；
| A．甲图中估测油酸分子直径时，可把油酸分子简化为球形处理 |
| B．乙图中，显微镜下看到的三颗微粒运动位置连线是它们做布朗运动的轨迹 |
| C．烧热的针尖，接触涂上薄蜂蜡层的云母片背面上某点，经一段时间后形成图丙的形状，则说明云母为非晶体 |
| D．丁图中分子间距离为r0时，分子间作用力F最小，分子势能也最小 |
（1）对于分子动理论和物体的内能理解，下列说法正确的是
A．液体表面的分子间距较大，所以表现为引力，液体表面有收缩的趋势
B．用力拉铁棒的两端，铁棒没有断，这是分子间存在吸引力的宏观表现
C．理想气体在状态变化时，温度升高，气体分子的平均动能增大，气体的压强也一定增大
D．当分子间的引力和斥力平衡时，分子势能最小
（2）如图所示P-V图，一定质量的理想气体由状态A经过程Ⅰ变至状态B时，从外界吸收热量420J同时膨胀对外做功300J．当气体从状态B经过程Ⅱ回到状态A时，外界压缩气体做功200J，求此过程中气体____________(填“吸收”或“放出”)热量为_________J
（3）某同学在进行“用油膜法估测分子的大小”的实验前，查阅数据手册得知：油酸的摩尔质量M=0.283kg·mol-1，密度ρ=0.895×103kg·m-3.若100滴油酸的体积为1ml，则1滴油酸所能形成的单分子油膜的面积约是多少？(取NA=6.02×1023mol-1.球的体积V与直径D的关系为
，结果保留一位有效数字)
12－2．（供选学3-4模块的考生做）
（1）以下是有关波动和相对论内容的若干叙述，其中正确的有（ ）
A．光速不变原理是：真空中的光速在不同的惯性参考系中都是相同的
B．两列波相叠加产生干涉现象，则振动加强区域与减弱区域交替变化
C．光的偏振现象说明光波是横波
D．夜视仪器能在较冷的背景上探测出较热物体的红外辐射
(2)一束光从空气射向折射率为
的某种介质，若反射光线与折射光线垂直，则入射角为__________。真空中的光速为c ，则光在该介质中的传播速度为________________ .
(3)将一劲度系数为K的轻质弹簧竖直悬挂，下端系上质量为m的物块，将物块向下拉离平衡位置后松开，物块上下做简谐运动，其振动周期恰好等于以物块平衡时弹簧的伸长量为摆长的单摆周期．请由单摆周期公式推算出物块做简谐运动的周期T．
利用油膜法可以粗略测出阿伏加德罗常数。把密度ρ＝0.8×103kg/m3的某种油，用滴管滴一滴在水面上形成油膜，已知这滴油的体积为V＝0.5×10－3cm3，形成的油膜面积为S＝0.7m2，油的摩尔质量M＝9×10－2kg/mol，若把油膜看成单分子层，每个油分子看成球形，那么：
（1）油分子的直径是多少？
（2）由以上数据可粗略测出阿伏加德罗常数NA是多少？（保留一位有效数字）
体积为1．2×10-3cm3的石油滴在平静的水面上，石油扩展为3m2的单分子油膜。试估算石油分子的直径约为____________m；估算出1mol石油的体积约为___________ m3。（结果保留一位有效数字，阿伏伽德罗常数NA=6.02×1023mol-1）
（1）已知某种气体的摩尔质量为M，密度为ρ，阿伏伽德罗常数为N。则该种气体中每个分子的质量为 ；分子的平均间距为 。
（2）如图甲所示，内径均匀、两端开口的U形管竖直放置，管中装入水银。稳定后，两管中水银面与管口的距离均为L=10cm。现将右侧管口密封，然后从左侧管口处将一活塞缓慢向下推入管中，直到左右两侧水银面高度差h=6cm时为止，如图乙所示。已知大气压强P0=75.8cmHg。求活塞在左管内竖直向下移动的距离。设管中气体温度不变。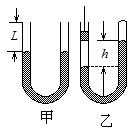
在做”用油膜法估测分子的大小”的实验中,实验简要步骤如下:
| A．根据油酸酒精溶液的浓度,算出一滴溶液中纯油酸的体积V. |
| B．用浅盘装入约2 cm深的水. |
| C．将一滴油酸酒精溶液滴在水面上,待油酸薄膜的形状稳定后,将玻璃板放在浅盘上,用彩笔将薄膜的形状描画在玻璃板上. |
| D．将画有油膜轮廓的玻璃板放在坐标纸上,数出轮廓内的方格数(不足半个的舍去,多于半个的算一个),再根据方格的边长求出油膜的面积S. |
E.用公式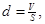
求出薄膜厚度,即油酸分子的大小.
上述步骤中有步骤遗漏或步骤不完全,请指出: (1)
(2)
已知水的密度
=1.0×10
kg/m，摩尔质量M=1.8×10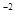
kg/mol，阿伏伽德罗常数NA=6.02×10
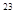mol
。
①每个水分子的质量约为 kg；
②估算每个水分子所占的体积。（计算结果均保留两位有效数字）
（模块3-3试题）
（1）液晶既具有液体的性质，又具有晶体的性质．液晶表面层的分子势能＿＿＿＿（选填“大于”、“等于”或“小于”）内部的分子势能；给液晶加热时，液晶的熵将＿＿＿＿（选填“增加”、“减少”或“不变”）．
（2）在“用油膜法估测分子的大小”的实验中，油酸酒精溶液的浓度为每104mL溶液中有纯油酸5mL．用注射器测得1mL上述溶液有液滴50滴．把1滴该溶液滴入盛水的浅盘里，待水面稳定后，将玻璃板放在浅盘上描出油膜轮廓，再将玻璃板放在坐标纸上，其形状如图所示，坐标纸中正方形小方格的边长为1cm．则：
①油膜的面积约为多少？（保留两位有效数字）
②每一滴油酸酒精溶液中含有纯油酸的体积是多少？
③根据上述数据，估算出油酸分子的直径．（保留一位有效数字）
下列说法正确的是（ ）
| A．知道水的摩尔质量和水分子的质量，可计算出阿伏加德罗常数 |
| B．当液晶中电场强度不同时，它对不同颜色的光吸收强度就不同 |
| C．蔗糖受潮后会粘在一起，没有确定的几何形状，它是非晶体 |
| D．理想气体的温度随时间不断升高，则其压强也一定不断增大 |
用油膜法估测分子的大小，方法及实验步骤如下：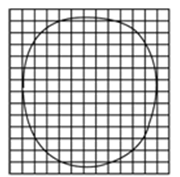
①向体积V油＝0.6 mL油酸中加酒精，直至总量达到V总＝1000 mL.
②用注射器吸取①中油酸酒精溶液，把它一滴一滴地滴入小量筒中，当滴入n＝80滴时，测得其体积恰好是V0＝1 mL.
③先往边长30～40 cm的浅盘里倒入2 cm深的水，然后将___________ 均匀地撒在水面上．[来④用注射器往水面上滴一滴油酸酒精溶液，待油酸在水面上尽可能散开，将事先准备好的带方格的塑料盖板放在浅盘上，并在塑料盖板上描下油酸膜的形状．
⑤描出的轮廓如图所示，已知每个小正方形的边长l＝10 mm，数出轮廓范围内正方形的个数，可以算出油酸膜的面积.
根据以上信息，回答下列问题
（1）完成步骤③中的填空；步骤④中要让油膜尽可能散开的原因是
（2）油酸膜的面积是_____ cm2；
（3）实验测出油酸分子的直径是________m；（最后一空计算结果保留两位有效数字）
若以μ表示水的摩尔质量，v表示在标准状态下水蒸气的摩尔体积，ρ表示在标准状态下水蒸气的密度，NA为阿伏加德罗常数，m、v0分别表示每个水分子的质量和体积。下列关系式中正确的是
A．NA= |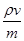
B．ρ= |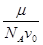
C．m= |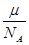
D．v0= |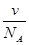
在“用油膜法估测分子大小”实验中所用的油酸酒精溶液的浓度为1 000 mL溶液中有纯油酸0.6 mL，用注射器测得1 mL上述溶液为80滴，把1滴该溶液滴入盛水的浅盘内，让油膜在水面上尽可能散开，测得油酸薄膜的轮廓形状和尺寸如图所示，图中正方形方格的边长为1 cm，试求：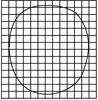
（1）油酸膜的面积是___________cm2；
（2）实验测出油酸分子的直径是___________m；（结果保留两位有效数字）
实验中为什么要让油膜尽可能散开？ ____________________
用油膜法可粗略测出阿伏加德罗常数，把密度ρ=0.8×103 kg/m3的某种油，用滴管滴出一滴油在水面上形成油膜，已知这滴油的体积V=0.5×10-3 cm3，形成的油膜的面积S="0.7" m2，油的摩尔质量Ml="0.09" kg/mol.若把油膜看成单分子层，每个油分子看成球形，那么：
(a)油分子的直径为多大？
(b)由以上数据可测出的阿伏加德罗常数大约为多少？（保留一位有效数字）
在“用油膜法测量分子直径”的实验中，将浓度为
的一滴油酸溶液，轻轻滴入水盆中，稳定后形成了一层单分子油膜．测得一滴油酸溶液的体积为V0，形成的油膜面积为S，则其中纯油酸的体积为 ，油酸分子的直径约为 ，如果把油酸分子看成是球形的（球的体积公式为
，d为球直径），该滴油酸溶液所含油酸分子数约为 ．
粤公网安备 44130202000953号