用两个相同的小量程电流表，分别改装成了两个量程不同的大量程电流表A1、A2，若把A1、A2分别采用并联或串联的方式接入电路，如图所示，则闭合电键后，下列有关电表的示数和电表指针偏转角度的说法正确的是( )
| A．图甲中的A1、A2的示数相同 |
| B．图甲中的A1、A2的指针偏角相同 |
| C．图乙中的A1、A2的示数和偏角都不同 |
| D．图乙中的A1、A2的指针偏角相同 |
在如图所示电路中，E为电源，其电动势为9.0 V，内阻可忽略不计；AB为滑动变阻器，其电阻R＝30 Ω；L为一小灯泡，其额定电压U＝6.0 V，额定功率P＝1.8 W；S为开关，开始时滑动变阻器的触头位于B端，现在闭合开关S.然后将触头缓慢地向A端滑动 ，当到达某一位置C处时，小灯泡刚好正常发光，则CB之间的电阻应为( )
| A．10 Ω | B．20 Ω |
| C．15 Ω | D．5 Ω |
如图所示，a、b分别表示由相同材料制成的两条长度相同、粗细均匀电阻丝的伏安特性曲线，下列判断中正确的是( )
| A．a代表的电阻丝较粗 |
| B．b代表的电阻丝较粗 |
| C．a电阻丝的阻值小于b电阻丝的阻值 |
| D．图线表示的电阻丝的阻值与电压成正比 |
根据经典理论，金属导体中电流的微观表达式为I＝nvSe，其中n为金属导体中每单位体积内的自由电子数，v为导体中自由电子沿导体定向移动的速率，S为导体的横截面积，e为自由电子的电荷量．如图11所示，两段长度和材料完全相同、各自粗细均匀的金属导线ab、bc，圆横截面的半径之比为rab∶rbc＝1∶4，串联后加上电压U，则 ( )
| A．两导线内的自由电子定向移动的速率之比为vab∶vbc＝1∶4 |
| B．两导线内的自由电子定向移动的速率之比为vab∶vbc＝4∶1 |
| C．两导线的电功率之比为Pab∶Pbc＝4∶1 |
| D．两导线的电功率之比为Pab∶Pbc＝16∶1 |
如图所示，闭合电键S，灯L1、L2正常发光，由于电路出现故障，突然发现灯L1变暗，电流表读数变小，则故障可能是
| A．R1断路 | B．R2断路 |
| C．R3短路 | D．R4短路 |
如图所示，将一光敏电阻接入多用电表两表笔上，将多用电表的选择开关置于欧姆挡，测光敏电阻时，表针的偏角（自左向右）为θ；现用手掌挡住部分光线，表针的偏角为θ′，则可判断( )
| A．θ′＝θ | B．θ′<θ |
| C．θ′>θ | D．不能确定 |
如图所示电路，电源内阻不可以忽略。开关S闭合后，在滑动变阻器的滑动端向上滑动的过程中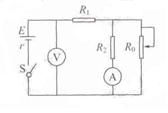
| A．电压表与电流表都减小 |
| B．电压表与电流表都增大 |
| C．电压表示数增大，电流表示数减小 |
| D．电压表示数减小，电流表示数增大 |
如图，甲电路可测出电压表内阻，已知电源内阻忽略不计，R为变阻箱，其取不同值时电压表示也变化，
图象如图乙，则电压表内阻Rv及电源电动势E为（ ）
A． k E=2V |
| B．kE=5V |
C． kE=50V |
| D．kE=2V |
如右图所示，因线路故障，按通K时，灯L1和L2均不亮，用电压表测得Uab=0，Ubc=0，Ucd=4V．由此可知开路处为
| A．灯L1 | B．灯L2 |
| C．变阻器 | D．不能确定 |
科学家费尔和格林贝尔由于发现“巨磁电阻”效应荣获2007年诺贝尔物理学奖。研究发现磁敏电阻(GMR)的阻值随所处空间磁场的增强而增大。图示电路中，GMR为一个磁敏电阻，闭合开关S1和S2，滑片P向右滑动时
| A．L1、L1都变暗 |
| B．L1、L2都变亮 |
| C．L1变暗，L2变亮 |
| D．L1变亮，L2变暗 |
两个定值电阻R1，R2串联后接在输出电压u，稳定等于12V的直 流电源上。有人把一个内阻不是远大于尺R1、R2的电压表接在R1两端，如图所示，电压表示数为8V。如果他把此电压表改接在R2两端，则电压表的示数将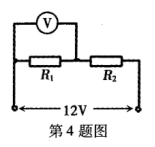
A．小于4V B．等于4V
c．大于4V小于8V D．等于或大于8V
如图所示，当滑动变阻器滑动触头向左滑动时，灯泡的亮度将( )
| A．都变亮 | B．都变暗 | C．A、B变暗，C变亮 | D．A、B变亮，C变暗 |
如图所示的U—I图像中，直线I为某电源的路端电压与电流的关系，直线Ⅱ为某一电阻R的伏安特性曲线，用该电源直接与电阻R连接成闭合电路，由图像可知 ( )
| A．R的阻值为1.5Ω |
| B．电源电动势为3V，内阻为0.5Ω |
| C．电源的输出功率为3.0w |
| D．电源内部消耗功率为1.5w |
如图所示电路中，三只灯泡原来都正常发光，当滑动变阻器的滑动触头P向右移动时，下面判断正确的是（ ）
| A．L1和L3变暗，L2变亮 |
| B．LI变暗，L2变亮，L3亮度不变 |
| C．L1中电流变化值大于L3中电流变化值 |
| D．Ll上电压变化值小于L2上的电压变化值 |
粤公网安备 44130202000953号