高中物理探究单摆的周期与摆长的关系选择题

一个单摆做受迫振动，其共振曲线（振幅A与驱动力的频率f的关系）如图所示，则 （ ）

A．此单摆的固有周期约为0.5s

B．此单摆的摆长约为2m

C．若摆长减小，单摆的固有频率增大

D．若摆长增大，共振曲线的峰将向左移动

如图所示为同一地点的两单摆甲、乙的振动图象，下列说法中正确的是________．（填正确答案标号，选对1个得3分，选对2个得4分，选对3个得6分；每选错1个扣3分，最低得分为0分）。

A．甲、乙两单摆的摆长相等

B．甲摆的振幅比乙摆大

C．甲摆的机械能比乙摆大

D．在t＝0.5s时有正向最大加速度的是乙摆

E．由图象可以求出当地的重力加速度

将一个电动传感器接到计算机上，就可以测量快速变化的力，用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图7所示．某同学由此图象提供的信息作出的下列判断中，正确的是（       ）

A．t＝0.2 s时摆球正经过最低点

B．t＝1.1 s时摆球正经过最低点

C．摆球摆动过程中机械能减小

D．摆球摆动的周期是T＝1.4 s

如图所示，两根细线长度均为2m，A细线竖直悬挂且在悬点O处穿有一个金属小球a，B悬挂在悬点处，细线下端系有一金属小球b，并且有m_a>m_b，把金属小球b向某一侧拉开3cm到处，然后同时让金属小球a、b由静止开始释放（不计阻力和摩擦），则两小球的最终情况是

A．a小球先到达最低点，不可能和b小球在最低点相碰撞；

B．b小球先到达最低点，不可能和a小球在最低点相碰撞；

C．a、b两小球恰好在最低点处发生碰撞；

D．因不知道ma、mb的具体数值，所以无法判断最终两小球的最终情况。

将一个力传感器接到计算机上，就可以测量快速变化的力，用这种方法测得的某单摆摆动时悬线上拉力的大小随时间变化的曲线如图所示。某同学由此图线提供的信息做出了下列判断
                                                    

A．s 时摆球正经过最高点

B．s 时摆球正经过最低点

C．摆球摆动过程中机械能守恒

D．摆球摆动的周期是 T＝1.2s

如图甲所示是用沙摆演示振动图像的实验装置，此装置可视为摆长为L的单摆，沙摆的运动可看作简谐运动，实验时在木板上留下图甲所示的结果。若用手拉木板做匀速运动，速度大小是v。图乙所示的一段木板的长度是s。下列说法正确的是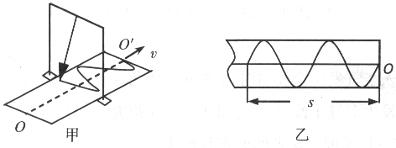

A．可估算出这次实验所用沙摆对应的摆长

B．若增大手拉木板的速度，则沙摆的周期将变大

C．若减小沙摆摆动时的最大摆角，则沙摆的周期将变小

D．若增大沙摆的摆长，保持拉动木板的速度不变，则仍将得到与图乙完全相同的图样

如图两单摆摆长相等，平衡时两摆刚好接触．现将摆球Ａ在两摆线所在平面内向左拉开一小角度后释放，碰撞后，两摆球分开各自做简谐运动．以 m_A、m_B分别表示摆球Ａ、Ｂ的质量，则

Ａ．如果m_A＞m_B，下一次碰撞将发生在平衡位置右侧
Ｂ．如果m_A＜m_B，下一次碰撞将发生在平衡位置左侧
Ｃ．无论摆球质量如何，下一次碰撞都不可能在平衡位置
Ｄ．无论摆球质量如何,下一次碰撞都不可能在平衡位置左侧或右侧

如图所示为同一实验室中两个单摆的振动图像。从图象可以知道它们的 （     ）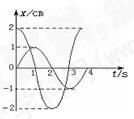

A．摆长相等

B．振幅相等

C．摆球同时改变速度方向

D．摆球质量差1 倍

如图所示，固定曲面AC是一段半径为4.0米的光滑圆弧形成的，圆弧与水平方向相切于A点，AB＝10cm，现将一小物体先后从圆弧顶端C和中点D处由静止释放，到达曲面低端时速度分别为v₁和v₂，所需时间为t₁和t₂，以下说法正确的是(    )

A．v1 > v2 , t1＝ t2	B．v1 > v2 , t1 > t2
C．v1 < v2 , t1＝ t2	D．v1 < v2 , t1 > t2

如图所示，放置在水平地面上的支架质量为M，支架顶端用细线拴着的摆球质量为m，现将摆球拉至水平位置，而后释放，摆球运动过程中，支架始终不动，以下说法正确的是（ ）

A．在释放前的瞬间，支架对地面的压力为（m+M）g

B．在释放前的瞬间，支架对地面的压力为mg

C．摆球到达最低点时，支架对地面的压力为（m+M）g

D．摆球到达最低点时，支架对地面的压力为（3m+M）g

一个弹簧振子，第一次被压缩x后释放做自由振动，周期为T₁，第二次被压缩2x后释放做自由振动，周期为T₂，则两次振动周期之比T₁∶T₂为（   ）

A．1∶2

B．1∶1

C．2∶1

D．1∶4

我国探月的“嫦娥工程”已启动，在不久的将来，我国宇航员将登上月球。假如宇航员在月球上测得摆长为l的单摆做小振幅振动的周期为T，将月球视为密度均匀、半径为r的球体，则月球的密度为

A．

B．

C．

D．

一个摆长为l₁的单摆，在地面上做简谐运动，周期为T₁，已知地球质量为M₁，半径为R₁，另一摆长为l₂的单摆，在质量为M₂，半径为R₂的星球表面做简谐运动，周期为T₂，若T₁＝2T₂，l₁＝4l₂，M₁＝4M₂，则地球半径与星球半径之比R₁∶R₂为（　　）

A．2∶1

B．2∶3

C．1∶2

D．3∶2

一个单摆和一个弹簧振子，在上海调节使得它们的振动周期相等(设为T)．现在把它们一起拿到北京，若不再做任何调节．设这时单摆的振动周期为T₁，弹簧振子的振动周期为T₂，则它们的周期大小的关系为(　　)．

A．T1<T2＝T

B．T1＝T2<T

C．T1>T2＝T

D．T1<T2<T

一绳长为L的单摆，在平衡位置正上方（L—L′）的P处有一个钉子，如图所示，这个摆的周期是