某同学要测量一根弹簧的劲度系数k,他先将待测弹簧的一端固定在铁架台上,当弹簧自然下垂时,用刻度尺测得弹簧的长度为L0,分别在弹簧下端挂上1个、2个和3个质量为m的砝码时,测得对应的弹簧的长度为L1、L2和L3.
下表是该同学记录的数据:
| 代表符号 |
L0 |
L1 |
L2 |
L3 |
| 刻度数值/cm |
5.70 |
7.40 |
9.15 |
10.95 |
(1)根据以上数据,计算出每增加一个砝码时弹簧平均伸长量△L的数值为△L= cm.
(2)已知重力加速度g,则计算该弹簧的劲度系数的表达式k= .
(3)若m=50g,g=9.8m/s2可求弹簧的劲度系数k= N/m.
鸵鸟是当今世界上最大的鸟。有人说它不会飞是因为翅膀退化了,如果鸵鸟长了一副与身体大小成比例的翅膀,它是否就能飞起来呢?这是一个使人极感兴趣的问题,试阅读下列材料并填写其中的空白处。
鸟飞翔的必要条件是空气的上举力F至少与体重G=mg平衡,鸟扇动翅膀获得的上举力可表示为  ,式中S为鸟翅膀的面积,v为鸟飞行的速度,c是恒量,鸟类能飞起的条件是
,式中S为鸟翅膀的面积,v为鸟飞行的速度,c是恒量,鸟类能飞起的条件是  ,即
,即  _________,取等号时的速率为临界速率。
_________,取等号时的速率为临界速率。
我们作一个简单的几何相似性假设。设鸟的几何线度为  ,质量
,质量  体积
体积  ,
,  ,于是起飞的临界速率
,于是起飞的临界速率  。燕子的滑翔速率最小大约为20 km/h,而鸵鸟的体长大约是燕子的25倍,从而跑动起飞的临界速率为________km/h,而实际上鸵鸟的奔跑速度大约只有40km/h,可见,鸵鸟是飞不起来的,我们在生活中还可以看到,像麻雀这样的小鸟,只需从枝头跳到空中,用翅膀拍打一两下,就可以飞起来。而像天鹅这样大的飞禽,则首先要沿着地面或水面奔跑一段才能起飞,这是因为_______,而天鹅的______。
。燕子的滑翔速率最小大约为20 km/h,而鸵鸟的体长大约是燕子的25倍,从而跑动起飞的临界速率为________km/h,而实际上鸵鸟的奔跑速度大约只有40km/h,可见,鸵鸟是飞不起来的,我们在生活中还可以看到,像麻雀这样的小鸟,只需从枝头跳到空中,用翅膀拍打一两下,就可以飞起来。而像天鹅这样大的飞禽,则首先要沿着地面或水面奔跑一段才能起飞,这是因为_______,而天鹅的______。
在地球表面上周期准确的秒摆(周期为2秒),移到距离地面为nR0的高度处(R0为地球半径),该秒摆的周期 秒,此时为了让秒摆保持周期2秒不变,则需要 (“增长”,“减短”)摆长.
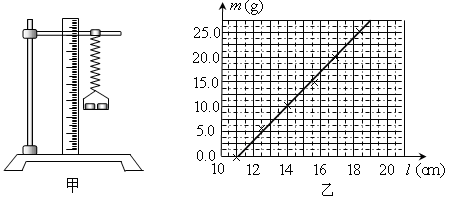
某同学利用如图甲所示的装置测量某一弹簧的劲度系数,将该弹簧竖直悬挂起来,在自由端挂上砝码盘。通过改变盘中砝码的质量,测得6组砝码的质量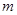 和对应的弹簧长度
和对应的弹簧长度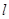 ,画出
,画出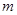 -
-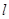 图线,对应点已在图上标出,如图乙所示。(重力加速度
图线,对应点已在图上标出,如图乙所示。(重力加速度 )
)
①采用恰当的数据处理,该弹簧的劲度系数为 ________ 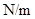 。(保留三位有效数字)
。(保留三位有效数字)
②请你判断该同学得到的实验结果与考虑砝码盘的质量相比,结果________。(填“偏大”、“偏小”或“相同”)
如图所示,一轻质弹簧原长为 ,钩码每一个重为
,钩码每一个重为 ,挂一个钩码时,弹簧的长为
,挂一个钩码时,弹簧的长为 ,则弹簧的劲度系数为
,则弹簧的劲度系数为  ,若挂3个钩码时,弹簧长为
,若挂3个钩码时,弹簧长为  (在弹簧弹性限度内)
(在弹簧弹性限度内)

做匀变速直线运动的质点,某阶段的初速度为v1,末速度为v2,则其在该过程的中点位置时的速度v= ;若已知该质点在另一阶段的前一半位移内平均速度为u1,后一半位移内的平均速度为u2, 则质点在此过程中间位置时的速度u= .
一辆汽车在平直的公路上先以10m/s的速度行驶300m,又以30m/s的速度向前行驶300m,则汽车在这600m过程中的平均速度大小为 m/s。
如图所示是某人在“用打点计时器测速度”实验中得到的纸带,纸带的右端后通过打点计时器.从点痕的分布情况可以断定纸带的运动情况是_______。若所用电源频率为50Hz,从打下A点到打下E点,共11点,历时_______s,位移为_______m,这段时间内纸带运动的平均速度是_______m/s.BD段的平均速度是_______m/s.
如图为“测量弹簧劲度系数”的实验装置图,弹簧的上端固定在铁架台上,下端装有指针及挂钩,指针恰好指向一把竖直立起的毫米刻度尺。现在测得在挂钩上挂上一定数量钩码时指针在刻度尺上的读数如下表:
| 钩码数n |
0 |
1 |
2 |
3 |
4 |
5 |
| 刻度尺读数xn(cm) |
2.62 |
4.17 |
5.70 |
7.22 |
8.84 |
10.43 |
已知所有钩码的质量可认为相同且为m0=50g,当地重力加速度g=9.8m/s2。请回答下列问题: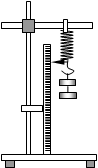
(1)请根据表格数据计算出弹簧的劲度系数,k =_____________N/m。(结果保留两位有效数字)
(2)考虑到在没有挂钩码时弹簧自身有重量,测量的劲度系数与真实值相比较__________(填偏大、偏小、没有影响)。