高中物理* 宇宙概观试题

“神州”号宇宙飞船绕地球做匀速圆周运动中，下述说法正确的是

A．宇宙飞船不受地球的吸引力作用

B．地球对宇宙飞船万有引力大小与飞船的质量有关系

C．地球对宇宙飞船的万有引力大小与飞船距离地面的高度平方成反比

D．宇宙飞船绕地球做匀速圆周运动的线速度必须大于地球第一宇宙速度

第一宇宙速度是（ ）

A．物体在宇宙中所能达到的最高速度

B．物体在地面附近绕地球做匀速圆周运动所必须具有的速度

C．物体摆脱地球引力所必须具有的速度

D．物体摆脱太阳引力所必须具有的速度

我们在推导第一宇宙速度的公式v＝时，需要做一些假设和选择一些理论依据，下列必要的假设和理论依据有  (　　)．

A．卫星做半径等于2倍地球半径的匀速圆周运动

B．卫星所受的重力全部作为其所需的向心力

C．卫星所受的万有引力仅有一部分作为其所需的向心力

D．卫星的运转周期必须等于地球的自转周期

(10分)已知火星表面附近的重力加速度为g，火星半径为R，火星自转周期为T。万有引力常量为G．求：
（1）火星上卫星的第一宇宙速度；
（2）火星的同步卫星距行星表面的高度h。

某星球的质量为地球质量的9倍，半径是地球半径的一半。若在地球上h高处平抛一物体，物体的落地点与抛出点的水平距离为60m，那么在该星球上，从同样高度以同样的初速度平抛物体，物体的落地点与抛出点的水平距离为：（  ）

A．10m

B．15m

C．40m

D．90m

一位同学为了测算卫星在月球表面附近做匀速圆周运动的环绕速度，提出了如下实验方案：在月球表面以初速度v₀竖直上抛一个物体，测出物体上升的最大高度h，已知月球的半径为R，便可测算出绕月卫星的环绕速度。按此方案，绕月卫星的环绕速度为 （ ）

A．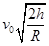

B．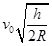

C．

D．

已知某天体的第一宇宙速度为8km/s，则距该天体表面高度为天体半径的宇宙飞船运行速度为_________km/s。

关于第一宇宙速度，下面说法正确的是

A．它是人造地球卫星绕地球飞行的最小速度

B．它是能使卫星进入近地圆形轨道的最大发射速度

C．它是地球同步卫星运动时的速度

D．所有绕地球做匀速圆周运动的人造卫星的速度都不可能大于第一宇宙速度

人造卫星绕地球做匀速圆周运动，对其线速度下列说法中正确的是（ ）

A．一定等于7.9km/s	B．等于或小于7.9km/s
C．一定大于7.9km/s	D．介于7.9km/s～11.2km/s

2007年10月24日18时05分，我国成功发射了“嫦娥一号”探月卫星，11月5日进入月球轨道后，经历三次轨道调整，进入工作轨道。若卫星在地球表面的重力为G₁，在月球表面的重力为G₂，已知地球半径为R₁，月球半径为R₂，地球表面处的重力加速度为g ,则（   ）    

A．月球表面处的重力加速度g月为

B．月球的质量与地球的质量之比为

C．卫星在月球表面轨道上做匀速圆周运动的周期T月为

D．月球的第一宇宙速度与地球的第一宇宙速度之比为

发射探测火星的飞船必须使飞船的速度超过第二宇宙速度．在下面的哪个地点、向什么方向发射，最节省能量？[　　]

A．发射场建在高纬度地区，向北方发射

B．发射场建在低纬度地区，向南方发射

C．发射场建在低纬度地区，向东方发射

D．发射场建在高纬度地区，向东方发射

三种宇宙速度分别是7.9km/s，11.2km/s，16.7km/s，则表明

A．物体绕地球做匀速圆周运动的最小速度是7.9km/s

B．物体绕地球做匀速圆周运动的最小速度是11.2km/s

C．物体绕地球做匀速圆周运动的最大速度是7.9km/s

D．物体绕太阳转动的最大速度是7.9km/s

在地球表面附近环绕地球运动的卫星，周期为85min，运动速度为7.9km/s。我国“风云”二号气象卫星，运动在赤道上方高度约为地球半径5.6倍的轨道上，关于该卫星的运动速度v和周期T，下列说法正确的是(     )

A．v<7.9km/s，T<85min	B．v<7.9km/s，T>85min
C．v>7.9km/s，T<85min	D．v>7.9km/s，T>85min

第一宇宙速度的数值为（）

A．

B．

C．

D．

海王星的质量是地球的17倍，它的半径是地球的4倍，则绕海王星表面做圆周运动的宇宙飞船，其运行速度是地球上第一宇宙速度的

A．17倍

B．4倍

C．倍

D．倍