高中物理* 宇宙概观选择题

我们在推导第一宇宙速度的公式v＝时，需要做一些假设和选择一些理论依据，下列必要的假设和理论依据有(　　)

A．卫星做半径等于2倍地球半径的匀速圆周运动

B．卫星所受的重力全部作为其所需的向心力

C．卫星所受的万有引力仅有一部分作为其所需的向心力

D．卫星的运转周期必须等于地球的自转周期

一位同学为了测算卫星在月球表面附近做匀速圆周运动的环绕速度，提出了如下实验方案：在月球表面以初速度v₀竖直上抛一个物体，测出物体上升的最大高度h，已知月球的半径为R，便可测算出绕月卫星的环绕速度。按此方案，绕月卫星的环绕速度为 （ ）

A．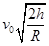

B．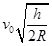

C．

D．

我国未来将在月球地面上建立月球基地，并在绕月轨道上建造空间站．如图所示，关闭发动机的航天飞机A在月球引力作用下沿椭圆轨道向月球靠近，并将在椭圆轨道的近月点B处与空间站C对接。已知空间站绕月圆轨道的半径为r，周期为T，万有引力常量为G，月球的半径为R。下列说法中错误的是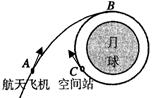

A．航天飞机在图示位置正在加速向B运动

B．月球的第一宇宙速度为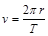

C．月球的质量为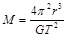

D．要使航天飞机和空间站对接成功，飞机在接近B点时必须减速

某卫星的发射过程如图所示，先将卫星从地面发射并从A点进入椭圆轨道I运行，然后在B点通过改变卫星的速度，让卫星进入预定圆形轨道II上运行。则下列说法正确的是（  ）

A．该卫星的发射速度一定要大于第二宇宙速度11.2km/s

B．该卫星沿椭圆轨道I从A点运动到B点过程中，速度减小，机械能增大

C．该卫星在轨道I上运行的周期大于在轨道II上运行的周期

D．测量出该卫星在轨道II上运行的线速度和周期，即可计算地球的质量

已知某天体的第一宇宙速度为8 km/s，则高度为该天体半径的宇宙飞船的运行速度为

A．km/s	B．4 km/s
C．km/s	D．8 km/s

我们在推导第一宇宙速度的公式v＝时，需要做一些假设和选择一些理论依据，下列必要的假设和理论依据有  (　　)．

A．卫星做半径等于2倍地球半径的匀速圆周运动

B．卫星所受的重力全部作为其所需的向心力

C．卫星所受的万有引力仅有一部分作为其所需的向心力

D．卫星的运转周期必须等于地球的自转周期

美国“新地平线”号探测器借助“宇宙神—5”火箭，从佛罗里达州卡纳维拉尔角肯尼迪航天中心发射升空，开始长达9年的飞向冥王星的太空之旅。拥有3级发动机的“宇宙神—5”重型火箭将以每小时5.76万公里的惊人速度把“新地平线”号送离地球，这个冥王星探测器将成为人类有史以来发射速度最高的飞行器。这一速度

A．大于第一宇宙速度	B．等于第二宇宙速度
C．大于第三宇宙速度	D．小于并接近于第三宇宙速度

一宇航员在某星球上以速度v₀竖直上抛一物体，经t秒落回原处，已知该星球半径为R，那么该星球的第一宇宙速度是

A．

B．

C．

D．

关于第一宇宙速度，下列说法中正确的是（   ）

A．它是人造地球卫星绕地球飞行的最小速度

B．它是卫星在椭圆轨道上运行时在近地点的速度

C．它是近地圆轨道上人造卫星的运行速度

D．它又叫环绕速度，即绕地球做圆轨道运行的卫星的速度都是第一宇宙速度

使物体脱离某星球的引力束缚，不再绕星球运行，从星球表面发射所需的最小速度称为第二宇宙速度，星球的第二宇宙速度v₂与第一宇宙速度v₁的关系是₁。已知某星球的半径为r，它表面的重力加速度为地球表面重力加速度g的。不计其他星球的影响，则该星球的第二宇宙速度为 

A．

B．

C．

D．

a、b、c、d四颗地球卫星，a还未发射，在地球赤道上随地球表面一起转动，向心加速度为a₁，b处于地面附近近地轨道上正常运动速度为v₁，c是地球同步卫星离地心距离为r，运行速率为v₂，加速度为a₂，d是高空探测卫星，各卫星排列位置如图2，地球的半径为R则有 (   )．

A．a的向心加速度等于重力加速度g

B．d的运动周期有可能是20小时

C．

D．

已知地球自转的角速度为7.29×10^－5 rad/s，月球到地球中心的距离为3.84×10⁸ m。在地球表面发射卫星的第一宇宙速度为7.9×10³ m/s，第二宇宙速度为11.2×10³ m/s，第三宇宙速度为16.7×10³ m/s，假设地球上有一棵苹果树长到了接近月球那么高，则当苹果脱离苹果树后，将：（     ）

A．落向地面	B．成为地球的同步“苹果卫星”
C．成为地球的“苹果月亮”	D．飞向茫茫宇宙

以下关于宇宙速度的说法中正确的是(        )
A第一宇宙速度是人造地球卫星发射时的最大速度  
B第一宇宙速度是人造地球卫星运行时的最小速度
C人造地球卫星运行时的速度一定小于第二宇宙速度
D地球上的物体无论具有多大的速度都不可能脱离太阳的束缚

使物体脱离星球的引力束缚，不再绕星球运行，从星球表面发射所需的最小速度称为第二宇宙速度，星球的第二宇宙速度v₂与第一宇宙速度v₁的关系是。已知某星球的半径为r，它表面的重力加速度为地球表面重力加速度g的1/6。不计其他星球的影响，则该星球的第二宇宙速度为 

A．

B．

C．

D．

举世瞩目的“神舟”六号航天飞船的成功发射和顺利返回，显示了我国航天事业取得的巨大成就，已知地球的质量为M，引力常量为G，设飞船绕地球做匀速圆周运动的轨道半径为r，则飞船在圆轨道上运行的速率为（    ）

A．

B．

C．

D．