、如图所示,实线是一列简谐横波在t1= 0时的波形图,虚线为t2=0.5s时的波形图,已知0<t2-t1<T,t1= 0时,x=2m处的质点A正向y轴正方向振动。
(1)质点A的振动周期为多少;
(2)求波的传播速度;
(3)从t2时刻计时,写出x=1m处的质点的振动方程。
如图所示,为波沿着一条固定的绳子向右刚传播到B点时的波形,由图可判断出A点刚开始的振动方向是 ( )
| A.向左 | B.向右 | C.向下 | D.向上 |
如图所示,为一在水平方向传播的简谐波,已知此时质点F向下运动,则以下说法正确的是( )
| A.波向右传播 |
| B.质点H与F的运动方向相同 |
| C.质点C比B先回到平衡位置 |
| D.此时质点C的加速度为0 |
如图所示为沿x轴正方向传播的一列简谐横波在某时刻的波形图,其波速为200m/s。下列说法中正确的是( )
| A.图示时刻质点b的加速度正在减小 |
| B.从图示时刻开始,经过0.01s质点b通过的路程小于0.4m |
C.若此波遇到另一波并发 生稳定干涉现象,则所遇到的波的频率为50Hz 生稳定干涉现象,则所遇到的波的频率为50Hz |
| D.若该波所遇到的障碍物的尺寸小于4m,则不能发生明显的衍射现象 |
(3-4)
(1)光线以某一入射角从空气射入折射率为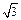 的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为
的玻璃中,折射光线与反射光线恰好垂直,则折射角等于____________;若光线以入射角α从折射率为 的某液体射入空气中正好发生全反射,入射角α等于___________________.
的某液体射入空气中正好发生全反射,入射角α等于___________________.
(2)如图所示,沿波的传播方向上有间距为1m的13个质点a.b.c.d.e.f.g.h.I.j.k.l.m,它们均静止在各自的平衡位置。一列横波以1m/s的速度水平向右传播,在t=0时刻到达质点a,且a开始由平衡位置向上振动,在t=1s时刻,质点a第一次达到最高点,求:
①这列波的波长和周期;
②从a开始振动,经过多长时间d点第一次向下达到最大位移;
③在上图中画出d点第一次向下达到最大位移时的波形图象。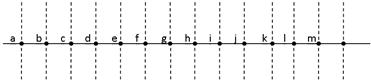
一质点做简谐运动的图象如图所示,下列判断中正确的是( )
| A.在t = 4s时质点速度达到最大值 |
| B.振幅为2cm,频率为0.25Hz |
| C.质点在0到1s的时间内,加速度和速度方向相同 |
| D.在t = 2s时,质点位移为负值,加速度也为负值 |
一列简谐波,在t=3s时刻的波形如图甲所示,图乙为波中一质点P1的振动图像,则以下判断不正确的是:
| A.该波向右传播 |
| B.该波的传播速度为6m/s |
| C.t=2s时,质点P2处于正向最大位移处 |
| D.t=10s时,质点P2处于平衡位置处 |
如图,沿 轴正方向传播的一列简谐横渡在某时刻的波形图为一正弦曲线,其波速为200 m/s,下列说法中错误的是 ( )
轴正方向传播的一列简谐横渡在某时刻的波形图为一正弦曲线,其波速为200 m/s,下列说法中错误的是 ( )
A.图示时刻质点 的加速度将减小 的加速度将减小 |
B.从图示时刻开始,经过0.0l s,质点 通过的路程为 通过的路程为 |
| C.若此波遇到另一列波并发生稳定于涉现象,则另一列波的频率为50 Hz |
| D.若该波传播中遇到宽约4 m的障碍物能发生明星的衍射现象 |
如图所示,实线是沿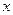 轴传播的一列简谐横波在
轴传播的一列简谐横波在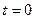 O时刻的波形图,虚线是这列波在
O时刻的波形图,虚线是这列波在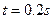 时刻的波形图。已知该波的波速是0.8m/s,则下列说法正确的是 ( )
时刻的波形图。已知该波的波速是0.8m/s,则下列说法正确的是 ( )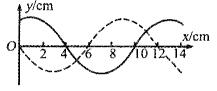
| A.这列波的波长是14 cm |
| B.这列波的周期是0.125 s |
C.这列波可能是沿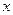 轴正方向传播的 轴正方向传播的 |
D.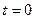 时, 时,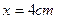 处的质点速度沿y轴负方向 处的质点速度沿y轴负方向 |
波速均为 的甲、乙两列同性质的简谐横波各自沿
的甲、乙两列同性质的简谐横波各自沿 轴正方向传播,某时刻波的图象分别如下图所示,其中质点P、Q均处于波峰。关于这两列波,下列说法正确的是 ( )
轴正方向传播,某时刻波的图象分别如下图所示,其中质点P、Q均处于波峰。关于这两列波,下列说法正确的是 ( )
| A.如果这两列波相遇,可能产生稳定的干涉图样 |
| B.甲波的周期大于乙波的周期 |
| C.甲波中的质点P比质点M先回到平衡位置 |
D.从图 示的时刻开始,经过1.0s,P、Q两质点通过的路程均为1.2m 示的时刻开始,经过1.0s,P、Q两质点通过的路程均为1.2m |
如图甲所示为一列简谐横波某一时刻的波形图,已知该波沿+x方向连续传播,传播速度为2m/s。求
(1)波形图上x=2m处的质点P的振动周期,并在图乙给出的坐标轴上画出从该时刻计时的振动图象(画出一个周期的图象,在坐标轴上须标明标度)
(2)如图丙所示的装置中,在探究共振现象的实验中发现;当作用在装置上MN间驱动力的频率与上述横波的频率相同时,MN间五个单摆中的D摆恰好发生共振。现测得D摆摆线长L0=99.6cm。摆球的直径d=0.8cm,则当地重力加速度g为多少大?(结果取3位有效数字)
一条弹性绳子呈水平状态,M为绳子中点,两端P、Q同时开始上下振动,一小段时间后产生的波形如图所示。已知机械波的传播速度由介质决定。对于其后绳上各点的振动情况,以下判断正确的是 ( )
| A.波源P的起振方向是向上的 |
| B.波源Q产生的波将先到达中点M |
| C.中点M的振动始终是加强的 |
| D.M点的位移大小在某时刻可能为零 |
如图所示是一列沿x轴正方向 传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
传播的简谐横波在t=0时刻的波形图,已知波的传播速度v=2m/s.试回答下列问题:
(1)该波的波长 为多大;
为多大;
(2)该波 的周期
的周期 为多大;
为多大;
(3)写出 处质点的振动函数表达式;
处质点的振动函数表达式;
(4)求出 处质点在0~4.5s内通过的路程
处质点在0~4.5s内通过的路程 及t=4.5s时刻的位移
及t=4.5s时刻的位移 。
。