图是最早的简易发电机──法拉第圆盘发电机.A为铜盘,OO'为转轴,磁感线穿过圆盘,圆盘在动力机带动下匀速转动时,轴与盘的边缘间产生电势差.若已知铜盘直径D=10cm,匀强磁场磁感强度B=1.0T,盘转速n="1800" r/min,计算盘转动时,发电机的感应电动势E的值.
如图所示,在磁感应强度为B的匀强磁场中,两根金属杆OM、ON在O点相接,夹角为120°。金属棒AC与两金属杆接触,接触点是E、F,△OEF是等腰三角形,EO=L。金属杆、金属棒单位长度的电阻都是K,现让AC以加速度a从静止开始垂直于AC向左运动,求回路中电功率的最大值。(已知磁场方向垂直△OEF所在平面)。
如图所示,水平放置的闭合圆形线圈,半径为a,磁场方向与线圈平面垂直.如果磁感强度的变化规律为B=Kt,线圈所用的导线截面积为b,导线的电阻率为ρ.求:在△t 时间内线圈所产生的热量.
用水平力F将矩形线框abcd水平向右以速度V匀速拉出磁场,开始时ab边和磁场边缘对齐,如下图所示,设匀强磁场的磁感强度为B,方向垂直纸面向里,试针对这一过程,用能量转化守恒定律导出法拉第电磁感应定律.
一个电阻为R的长方形线圈abcd沿着磁针所指的南北方向平放在北半球的一个水平桌面上,ab=L1,bc=L2,如图所示。现突然将线圈翻转1800,使ab与dc互换位置,用冲击电流计测得导线中流过的电量为Q1。然后维持ad边不动,将线圈绕ad边转动,使之突然竖直,这次测得导线中流过的电量为Q2,试求该处地磁场的磁感强度的大小。
如图所示,两根相距为L的竖直平行金属导轨位于磁感应强度为B、方向垂直纸面向里的匀强磁场中,导轨电阻不计,另外两根与上述光滑导轨保持良好接触的金属杆ab、cd质量均为m,电阻均为R,若要使cd静止不动,则ab速度大小为多大?作用于ab杆上的外力大小为多大?
如图所示,固定于水平面上的金属框cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动.此时abed构成一个边长l的正方形,棒电阻r,其余电阻不计,开始时磁感应强度为B。
(1)若以t=0时起,磁感应强度均匀增加,每秒增加量k,同时保持棒静止,求棒中的感应电流。
(2)在上述情况中,棒始终保持静止,当t=t1时需加垂直于棒水平外力多大?
(3)若从t=0时起,磁感应强度逐渐减小,当棒以恒定速度v向右匀速运动,可使棒中不产生I感,则磁感应强度应怎样随时间变化?(写出B与t的关系式)
如图所示,有一弯成θ角的光滑金属导轨POQ,水平放置在磁感应强度为B的匀强磁场中,磁场方向与导轨平面垂直,有一金属棒MN与导轨的OQ边垂直放置,当金属棒从O点开始以加速度a向右匀加速运动t秒时,棒与导轨所构成的回路中的感应电动势是多少?
如图所示,竖直放置的光滑平行金属导轨MN、PQ相距L,在M点和P点间接一个阻值为R的电阻,在两导轨间OO1O1′O′ 矩形区域内有垂直导轨平面向里、宽为d的匀强磁场,磁感应强度为B.一质量为m,电阻为r的导体棒ab垂直搁在导轨上,与磁场上边边界相距d0.现使ab棒由静止开始释放,棒ab在离开磁场前已经做匀速直线运动(棒ab与导轨始终保持良好的电接触且下落过程中始终保持水平,导轨电阻不计).求:
棒ab在离开磁场下边界时的速度;
棒ab在通过磁场区的过程中产生的焦耳热;
试分析讨论ab棒在磁场中可能出现的运动情况。
如图所示,足够长的光滑平行金属导轨cd和ef,水平放置且相距L,在其左端各固定一个半径为r的四分之三金属光滑圆环,两圆环面平行且竖直。在水平导轨和圆环上各有一根与导轨垂直的金属杆,两金属杆与水平导轨、金属圆环形成闭合回路,两金属杆质量均为m,电阻均为R,其余电阻不计。整个装置放在磁感应强度大小为B、方向竖直向上的匀强磁场中。当用水平向右的恒力F= mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
mg拉细杆a,达到匀速运动时,杆b恰好静止在圆环上某处,试求:
(1)杆a做匀速运动时,回路中的感应电流;
(2)杆a做匀速运动时的速度;
(3)杆b静止的位置距圆环最低点的高度。 
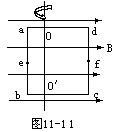
用均匀导线弯成正方形闭合金属线框abcd,线框每边长80cm,每边的电阻为0.01Ω。把线框放在磁感强度B=0.05T的匀强磁场中,并使它绕轴OO′以ω=100rad/s的角速度匀角速度旋转,旋转方向如图
(1)每条边产生的感应动势大小;
(2)线框内感应电流的大小;
(3)e,f分别是ab和cd的中点,ef两点间的电势差。