电场线分布如图所示,电场中a,b两点的电场强度大小分别为Ea和Eb,电势分别为φa和φb,则( )

| A.Ea<Eb,φa<φb | B.Ea>Eb,φa<φb |
| C.Ea<Eb,φa>φb | D.Ea>Eb,φa>φb |
关于静电场下列说法中正确的是
| A.在电场中某点的电势为零,则该点的电场强度一定为零 |
| B.电荷在电场中电势高的地方电势能大,在电势低的地方电势能小 |
| C.根据公式U=Ed知,在匀强电场中两点间的距离越大,电势差就越大 |
| D.正电荷从电势高的点运动到电势低的点,电势能一定减少 |
一长为L=1m的绝缘细线,上端固定,下端拴一质量为m=0.1kg、带电荷量为 的小球,处于如图所示的水平向右的匀强电场中,形如时,将线与小球向右拉成水平,然后释放,小球由静止开始向下摆动,当细线转过60o角时,小球到达B点速度恰好为零。(g=10m/s2)试求:
的小球,处于如图所示的水平向右的匀强电场中,形如时,将线与小球向右拉成水平,然后释放,小球由静止开始向下摆动,当细线转过60o角时,小球到达B点速度恰好为零。(g=10m/s2)试求:
(1)AB两点的电势差UAB;
(2)匀强电场的场强大小;
(3)小球从A到B过程中,最大速度多大?
如图所示,真空中同一平面内MN直线上固定电荷量分别为-9Q和+Q的两个点电荷,两者相距为L,以+Q电荷为圆心,半径为 画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为q的负试探电荷在圆周上运动,比较a、b、c、d四点,则下列说法正确的是( )
画圆,a、b、c、d是圆周上四点,其中a、b在MN直线上,c、d两点连线垂直于MN,一电荷量为q的负试探电荷在圆周上运动,比较a、b、c、d四点,则下列说法正确的是( )

A.a点电场强度最大
B.电荷q在b点的电势能最大
C.c、d两处的电势能相等
C.电荷q在a点的电势能最大
在x轴上存在与x轴平行的电场,x轴上各点的电势随x点位置变化情况如图所示。图中的-x1---x2之间为曲线,且关于纵轴对称,其余均为直线,也关于纵轴对称。下列关于该电场的论述正确的是( )

| A.x轴上各点的场强大小相等 |
| B.从-x1到x1场强的大小先减小后增大 |
| C.一个带正电的粒子在x1点的电势能大于在-x1点的电势能 |
| D.一个带正电的粒子在-x1点的电势能小于在-x2点的电势能 |
某点电荷和金属圆环间的电场线分布如图所示,下列说法正确的是( )

| A.a点的电势高于b点的电势 |
| B.若将一正试探电荷由a点移到b点,电场力做负功 |
| C.c点的电场强度与d点的电场强度大小无法比较 |
| D.若将一正试探电荷从d点由静止释放,电荷将沿着电场线由d到c |
如图所示, — x图表示空间某一静电场的电势
— x图表示空间某一静电场的电势 沿x轴的变化规律,图像关于
沿x轴的变化规律,图像关于 轴对称分布。x轴上a、b两点电场强度在x方向上的分量分别是Eax、Ebx,则
轴对称分布。x轴上a、b两点电场强度在x方向上的分量分别是Eax、Ebx,则
| A.Eax<Ebx |
| B.Eax沿x负方向,Ebx沿x正方向 |
| C.同一点电荷在a、b两点受到的电场力方向一定相反 |
| D.将正电荷沿x轴从a移动到b的过程中,其电势能先增加后减小 |
如图所示,在直角坐标系点(2,0)处固定一个电荷量为+2q的点电荷,点(-2,0)处固定一个电荷量为-q的点电荷。下列说法正确的是
| A.在x轴上电场强度为零的点有两个 |
B.图中(0,2)点的电场强度大小是 |
| C.(0,0)点的电势一定高于(0,2)点的电势 |
| D.将一个正电荷从(1,1)点移动到(-2,-1)点,电势能增大 |
在光滑绝缘水平面的P点正上方O点固定一电荷量为+Q的点电荷,在水平面上的N点,由静止释放质量为m,电荷量为-q的检验电荷,该检验电荷经过P点时速度为v,图中 ,则在+Q形成的电场中(固定P点的电势为零)
,则在+Q形成的电场中(固定P点的电势为零)
| A.N点的电势为正 |
B.N点的电势为 |
| C.P点电场前度大小是N点的2倍 |
D.检验电荷在N点具有的电势能为 |
如图所示,点电荷q只在Q的电场力作用下沿椭圆轨道运动,Q位于椭圆轨道的一个焦点上,则关于点电荷q的下列说法正确的是( )

| A.从M点运动到N点的过程中电势能增加 |
| B.从M点运动到N点的过程中动能增加 |
| C.q在M点的加速度比N点的加速度大 |
| D.从M点运动到N点,电势能与动能之和增加 |
如图所示,在竖直放置的光滑半圆绝缘吸管的圆心O处放一点电荷,其电荷量未知。将质量为m、电荷量为+q的小球从圆弧管的水平直径端点A由静止释放,小球沿细管滑到最低点B时,对管壁恰好无作用力,则下列说法中正确的是
A.B点的场强为 |
| B.O点处电荷是正电荷 |
| C.小球在A点的电势能大于B点的电势能 |
| D.小球恰能到达水平直径的C端 |
一平行电容器,两板间的距离为d,所带电荷量为Q时两极板间电势差为 ,板间场强为
,板间场强为 ;现将电容器所带电荷量增加一倍,板间距离变为原来的一半,其他条件不变,这时两极板间的电势差为
;现将电容器所带电荷量增加一倍,板间距离变为原来的一半,其他条件不变,这时两极板间的电势差为 ,板间场强为
,板间场强为 ,下列说法正确的是
,下列说法正确的是
A. |
B. |
C. |
D. |
如图甲所示,两个带正电的小球A、B套在一个倾斜的光滑直杆上,两球均可视为点电荷,其中A球固定,带电量QA=2×10﹣4C,B球的质量为m=0.1kg.以A为坐标原点,沿杆向上建立直线坐标系,B球的总势能随位置x的变化规律如图中曲线Ⅰ所示,直线Ⅱ为曲线I的渐近线.图中M点离A点距离为6米.(g取10m/s2,静电力恒量k=9.0×109N•m2/C2.)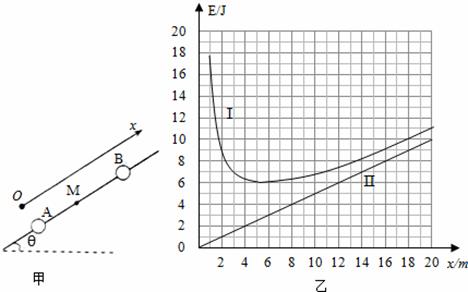
(1)求杆与水平面的夹角θ;
(2)求B球的带电量QB;
(3)求M点电势φM;
(4)若B球以Ek0=4J的初动能从M点开始沿杆向上滑动,求B球运动过程中离A球的最近距离及此时B球的加速度.