高中物理库仑定律选择题

如图所示，足够大的光滑绝缘水平面上有三个带电质点，A和C围绕B做匀速圆周运动，B恰能保持静止，其中A、C和B的距离分别是L₁和L₂．不计三质点间的万有引力，则A和C的比荷（电量与质量之比）之比应是(     )

A．          B．            C．         D．  

水平面上A、B、C三点固定着三个电荷量均为Q的正点电荷，将另一质量为m的带正电的小球（可视为点电荷）放置在O点，OABC恰构成一棱长为L的正四面体，如图所示。已知静电力常量为k，重力加速度为g，为使小球能静止在O点，小球所带的电荷量为

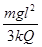A． B． C． D．

如图所示，A、B两球所带电荷量均为C，质量均为0.72kg，其中A球带正电荷，B球带负电荷，A球通过绝缘细线吊在天花板上，B球一端固定绝缘棒，现将B球放在某一位置，能使绝缘细线伸直，A球静止且与竖直方向的夹角为30°，则A、B两球之间的距离可能为（   ）

A．0.5m           B．0.8m          C．1.2m            D．2.5m

如图所示，A、B两球大小不计，所带电荷量均为C，质量均为0.72kg，其中A球带正电荷，B球带负电荷，A球通过绝缘细线吊在天花板上，B球一端固定绝缘棒，现将B球放在某一位置，能使绝缘细线伸直，A球静止且与竖直方向的夹角为30°，则A、B两小球之间的距离可能为

A．0.8m           B．1.2m          C．2m            D．2.5m

在物理学理论建立的过程中，有许多伟大的科学家做出了贡献．关于科学家和他们的贡献，下列说法中正确的是

A．法拉第根据电流的磁效应现象得出了法拉第电磁感应定律

B．卡文迪许发现了电荷之间的相互作用规律，并测出了静电力常量k的值

C．开普勒通过研究行星观测记录，发现了行星运动三大定律

D．牛顿总结出了万有引力定律并用实验测出了引力常量

如图，足够大的光滑绝缘水平面上有三个带电质点，A和C围绕B做匀速圆周运动，B恰能保持静止，其中A、C和B的距离分别是L₁和L₂．不计三质点间的万有引力，则A和C的比荷（电量与质量之比）之比应是(     )

A．          B．            C．         D．  

如图所示，一质量为m的带电小球A用长度为l的绝缘丝质细线悬挂于天花板上的O点，在O点的正下方l处的绝缘支架上固定一个带与A同种电荷的小球B，两个带电小球都可视为点电荷．已知小球A静止时丝线OA与竖直方向的夹角为60°，设丝线中拉力为T，小球所受库仑力为F，下列关系式正确的是

A．

B．

C．

D．

如图所示，竖直墙面与水平地面均光滑且绝缘。两个质量均为m、带有电量为q_A、q_B（q_A≠q_B）的同种电荷的小球A、B分别处于竖直墙面和水平地面，且处于同一竖直平面内，用图示方向的水平推力F作用于小球B，两球静止于图示位置，此时两小球之间的距离为l。下面的结论或论述正确的是

A．
B．
C．若将两小球A、B接触后再放置在原位置，其他条件不变，两小球A、B仍能保持平衡
D．若将两小球A、B接触后再放置在原位置，其他条件不变，两小球A、B不可能保持平衡

两个相同的金属小球（均可看做点电荷），原来所带的电荷量分别为+5q和-q，相互间的库仑力大小为F．现将它们相接触，再分别放回原处，则两金属小球间的库仑力大小变为
Ａ．9F/5   B．F   C．4F/5   D．F/5

关于点电荷的说法，正确的是（ ）

A．只有体积很小的电荷，才能作为点电荷

B．体积很大的电荷，一定不能作为点电荷

C．点电荷一定是带电量很小的电荷

D．两个带电的金属小球，不一定能将它们作为电荷集中在球心的点电荷处理

如图，在正点电荷Q形成的电场中，在某点M放入一电荷量为q的正点电荷P，P受到的库仑力为F，下列表述正确的是(      )

A．P、Q之间相互吸引

B．若将P移走，则M点的电场强度为零

C．若将P移近Q，则P所受库仑力减小

D．若将P的电荷量增大为2q，则P所受库仑力增大为2F

两个分别带有电荷量和+的相同金属小球（均可视为点电荷），固定在相距为的两处，它们间库仑力的大小为F。两小球相互接触后将其固定距离变为r/2，则两球间库仑力的大小为(    )     

A．

B．

C．

D．

如图示，相互垂直的固定绝缘光滑挡板PO、QO，竖直放置在重力场中，a、b为两个带有同种电量的小球（可以近似看成点电荷），当用水平向左作用力F作用于b时，a、b紧靠挡板处于静止状态。现若稍改变F的大小，使b稍有向左移动一段小距离，则当a、b重新处于静止状态后（ ）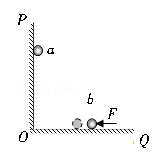

A．b间的电场力增大	B．作用力F将减小
C．系统重力势能增加	D．系统的电势能将增加

如图所示，两条绝缘细线一端拴在同一点，另一端分别拴两个带同种电荷的小球A、B，电荷量分别为q₁、q₂，质量分别为m₁、m₂，当小球A、B静止时恰好处于同一水平面，两细线与竖直方向的夹角分别为θ₁、θ₂，则

A．若m₁＝m₂，则θ₁＝θ₂         B．若m₁＞m₂，则θ₁＞θ₂
C．若q₁＝q₂，则θ₁＝θ₂          D．若q₁＞q₂，则θ₁＞θ₂

有两个完全一样的金属小球A.B，带电量Q_A=2×10^-9C，Q_B=-3×10^-9C，固定于相距为r的两点上，A.B间作用力为F。用一带绝缘柄的不带电的并且与A.B等大的金属球C先去接触A，再同B接触，最后移去C，则此时A.B间作用力为（   ）
A. F/2           B. F/4           C. F/5          D. F/6