如图所示，光滑绝缘水平桌面上有A、B两个带电小球（可以看成点电荷），A球带电量为+2q，B球带电量为-q，将它们同时由静止开始释放，A球加速度的大小为B球的3倍．现在AB中点固定一个带电小球C（也可看作点电荷），再同时由静止释放A、B两球，释放瞬间两球加速度大小相等．则C球带电量可能为 （ ）
A．
q B．
q C．
q D．
q
如图所示，在直线MN上有一个点电荷，A、B是直线MN上的两点，两点的间距为L，场强大小分别为E和2E.则（ ）
A．该点电荷一定在A点的右侧
B．该点电荷一定在A点的左侧
C．A点场强方向一定沿直线向左
D．A点的电势一定低于B点的电势
如图，有一带电荷量为＋q的点电荷与表面均匀带电圆形绝缘介质薄板相距为2d，此点电荷到带电薄板的垂线通过板的圆心。若图中a点处的电场强度为零，则图中b点处的电场强度大小是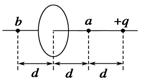
| A．0 | B． |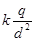
C． |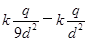
D． |
如图所示，在a、b两点上放置两个点电荷，它们的电荷量分别为q1、q2，MN是连接两点的直线，P是直线上的一点，下列情况下P点的场强可能为零的是( )
| A．q1、q2都是正电荷，且q1>q2 |
| B．q1是正电荷，q2是负电荷，且q1<|q2| |
| C．q1是负电荷，q2是正电荷，且|q1|>q2 |
| D．q1、q2都是负电荷，且|q1|<|q2| |
在人们探究物理科学的道路上，许多科学家做出了不懈的努力，下列所描述的事实正确的是
| A．牛顿首先阐明了运动的相对性原理，初次测光速未获成功，而开普勒在《宇宙和谐论》中提出开普勒第三定律 |
| B．法国物理学家库仑用他自己发明的扭秤，从实验得到静电力的平方反比定律，库仑定律是电学发展史上的第一个定量规律，是电学史中的一块重要的里程碑 |
| C．安培发现磁场对运动电荷的作用规律 |
| D．德国物理学家韦伯发现自感，对电磁学有独创性的研究 |
如右图， M、N和P是以 MN为直径的半圈弧上的三点，O点为半圆弧的圆心，
．电荷量相等、符号相反的两个点电荷分别置于M、N两点，这时O点电场强度的大小为E1；若将N点处的点电荷移至P点，则O点的场场强大小变为E2，E1与E2之比为( )
| A．1:2 | B．2:1 | C． |
D． |
如图所示，光滑绝缘水平面上有三个带电小球A、B、C（可视为点电荷），三球沿一条直线摆放，仅在它们之间的静电力作用下静止，则以下判断正确的是（ ）
A．A对B的静电力一定是引力
B．A对B的静电力可能是斥力
C．A的电量可能比B少
D．C的电量一定比B少
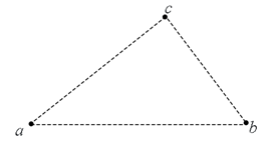
如图，三个固定的带电小球a、b和c，相互间的距离分别为 ， ， 。小球c所受库仑力的合力的方向平行于a、b的连线。设小球a、b所带电荷量的比值的绝对值为K，则（ ）。
| A． |
a、b的电荷同号， |
B． |
a、b的电荷异号， |
| C． |
a、b的电荷同号， |
D． |
a、b的电荷异号， |
有两个完全相同的金属球A、B，B球固定在绝缘地板上，A球在离B球为H的正上方由静止释放下落，与B球发生对心正碰后回跳的高度为h．设碰撞中无动能损失，空气阻力不计，若（ ）
A．A、B球带等量同种电荷，则h＞H
B．A、B球带等量同种电荷，则h=H
C．A、B球带等量异种电荷，则h＞H
D．A、B球带等量异种电荷，则h=H
可视为点电荷的A、B两带电小球固定在真空中，所带电荷量均为+q，若仅将A球所带电量变为﹣q，则B球所受的库仑力（ ）
A．大小和方向均不变 B．大小和方向均改变
C．大小改变、方向不变 D．大小不变、方向改变
真空中有两个相同的带电金属小球A和B，相距为r，带电量分别为q和2q，它们之间相互作用力的大小为F．有一个不带电的金属球C，大小跟A.B相同，当C跟A.B小球各接触一次后拿开，再将A.B间距离变为2r，那么A.B间的作用力的大小可为（ ）
A．5F/64 B．0 C．3F/32 D．5F/16
如图示，相互垂直的固定绝缘光滑挡板PO、QO，竖直放置在重力场中，a、b为两个带有同种电量的小球（可以近似看成点电荷），当用水平向左作用力F作用于b时，a、b紧靠挡板处于静止状态。现若稍改变F的大小，使b稍有向左移动一段小距离，则当a、b重新处于静止状态后（ ）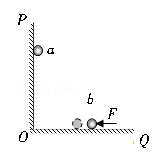
| A．b间的电场力增大 | B．作用力F将减小 |
| C．系统重力势能增加 | D．系统的电势能将增加 |
半径为R的均匀带电细圆环的电荷量为Q。在过圆一环中心O与圆环平面垂直的轴线上放一电荷量为q的点电荷，点电荷到圆环中心的距离为x。点电荷受到的库仑力是
A． |
B． |
C． |
D． |
粤公网安备 44130202000953号