高中物理电荷守恒定律选择题

玩具弹力球（如图）具有较好的弹性，碰撞后能等速反向弹回。一小孩将弹力球举高后由静止释放做自由落体运动，与水平地面发生碰撞，弹力球在空中往返运动。若从释放弹力球时开始计时，且不计弹力球与地面发生碰撞的时间和空气阻力，则弹力球运动的速度时间--图线是

如图所示，物体A、B静止在光滑的水平面上，其中A、B质量相等且B以速度V向A运动，A的左端连着一根弹簧，最终A、B沿着同一条直线运动，则他们系统动能损失最大的时候是（ ）
A．A刚开始压缩弹簧时     B．A的速度等于v时
C．B的速度等于零时      D．弹簧压缩最短时

台球以10m/s的速度垂直撞击框边后以8m/s的速度反向弹回，若地球与框边的接触时间为0.1s，（取初速度方向为正方向）下列说法正确的是（ ）

A．此过程速度改变量为2m/s

B．此过程速度改变量为18m/s

C．台球在水平方向的平均加速度大小为20m/s^2，方向沿球弹回的方向

D．台球在水平方向的平均加速度大小为180m/s^2，方向沿球弹回的方向

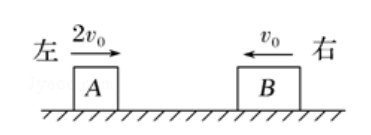
如图，两滑块 $A$ 、 $B$ 在光滑水平面上沿同一直线相向运动，滑块 $A$ 的质量为 $m$ ，速度为 $2v_0$ ，方向向右，滑块B的质量为 $2m$ ，速度大小为 $v_0$ ，方向向左，两滑块发生弹性碰撞后的运动状态是 （）    

A．	$A$ 和 $B$ 都向左运动	B．	$A$ 和 $B$ 都向右运动
C．	$A$ 静止， $B$ 向右运动	D．	$A$ 向左运动， $B$ 向右运动

如图所示，相距l的两小球A、B位于同一高度h（l、h均为定值）。将A向B水平抛出的同时，B自由下落。A、B与地面碰撞前后，水平分速度不变，竖直分速度大小不变、方向相反。不计空气阻力及小球与地面碰撞的时间，则

A．A、B在第一次落地前能否发生相碰，取决于A的初速度大小
B．A、B在第一次落地前若不相碰，此后就不会相碰
C．A、B不可能运动到最高处相碰
D．A、B一定能相碰

如图所示， 一个倾角为α的直角斜面体静置于光滑水平面上，斜面体质量为M，顶端高度为h.今有一质量为m的小物块，沿光滑斜面下滑，当小物块从斜面顶端自由下滑到底端时，斜面体在水平面上移动的距离是（  ）

A．

B．

C．

D．

台球以10m/s的速度沿与框边垂直的方向撞击后以8m/s的速度反向弹回．若球与框边的接触时间为0.1s，则台球在与边框碰撞的过程中，它的平均加速度大小和方向为（ ）

A．20m/s^2沿球弹回的方向	B．20m/s^2沿球撞击的方向
C．180m/s^2沿球弹回的方向	D．180m/s^2沿球撞击的方向

装有炮弹的大炮总质量为M，炮弹的质量为m，炮弹射出炮口时对地的速度为v0，若炮筒与水平地面的夹角为θ，则炮车后退的速度大小为（   ）

A．

B．

C．

D．

一颗子弹以水平速度穿透一块在光滑水平面上迎面滑来的木块后，二者运动方向均不变，设子弹与木块间相互作用力恒定，木块最后速度为v，则

A．越大，v越大	B．越小，v越大
C．子弹质量越小，v越大	D．木块质量越大，v越大

某人从高为5m处以某一初速度竖直向下抛一小球，在与地面相碰后弹起，上升到高为2m处被接住，则这段过程中（ ）

A．小球的位移为3m，方向竖直向下，路程为7m

B．小球的位移为7m，方向竖直向上，路程为7m

C．小球的位移为3m，方向竖直向下，路程为3m

D．小球的位移为7m，方向竖直向上，路程为3m

从手中竖直向上抛出的小球，与水平天花板碰撞后又落回到手中，设竖直向上的方向为正方向，小球与天花板碰撞时间极短．若不计空气阻力和碰撞过程中动能的损失，则下列图象中能够描述小球从抛出到落回手中整个过程运动规律的是（ ）

A．

B．

C．

D．

如图，质量为的木板放在光滑水平面上，质量为的物块放在木板上，它们之间有摩擦，木板足够长，两者都以的初速度向相反方向运动，当木板的速度为向右时，物块做（  ）

A．匀速运动	B．加速运动
C．减速运动	D．静止不动

质量为1kg的小球A以4m/s的速度与质量为2kg的静止小球B正碰。关于碰后A、B的速度v₁’与v₂’_’，下面哪些是可能的：（     ）
A. v₁’＝v₂’＝4/3m/s；     B. v₁’＝－1m/s，v₂’＝2.5m/s
C. v₁’＝1m/s，v₂’＝3m/s； D. v₁’＝－4m/s，v₂’＝4m/s

如果一个系统不受外力，或者所受外力的矢量和为零，这个系统的总动量保持不变。这就是动量守恒定律。若一个系统动量守恒时，则

A．此系统内每个物体所受的合力一定都为零

B．此系统内每个物体的动量大小不可能都增加

C．此系统的机械能一定守恒

D．此系统的机械能可能增加

如图所示，水平地面上固定有两块木板AB、BC，两块木板紧挨在一起，木板AB的长度是BC的3倍．一颗子弹以初速度v₀从A端水平射入木板，并恰能从C端射出，经历的时间为t，子弹在木板中的运动可以看成匀减速运动，则下列说法中正确的是（ ）

A．子弹到达B点时的速度为
B．子弹到达B点时的速度为
C．子弹从A到B所用的时间为
D．子弹从A到B所用的时间为